面向开发工程师的 0 基础机器学习教程 - 神经网络(三)
面向开发工程师的 0 基础机器学习教程 - 神经网络(三)
接上次最简单的「与门」三维空间机器学习算法后,可以分自然地联想到「或门」、「非门」、「异或门」,随着实践的进行,你会发现在「或门」、「非门」还是非常顺畅的,但到了「异或门」,还是遇到了模型预测定义不够好的问题,即损失函数无法再下降的前提下,拟合还是太差。这个时候,机器学习下的一个分支,「深度学习」就要开始发挥他的作用了[1]。
异或门的特别之处
直观地理解其中差距,可以看「异或门」训练之后的平面,始终无法正确拟合所有的数据点,如下:
| 与门 | 异或门 |
|---|---|
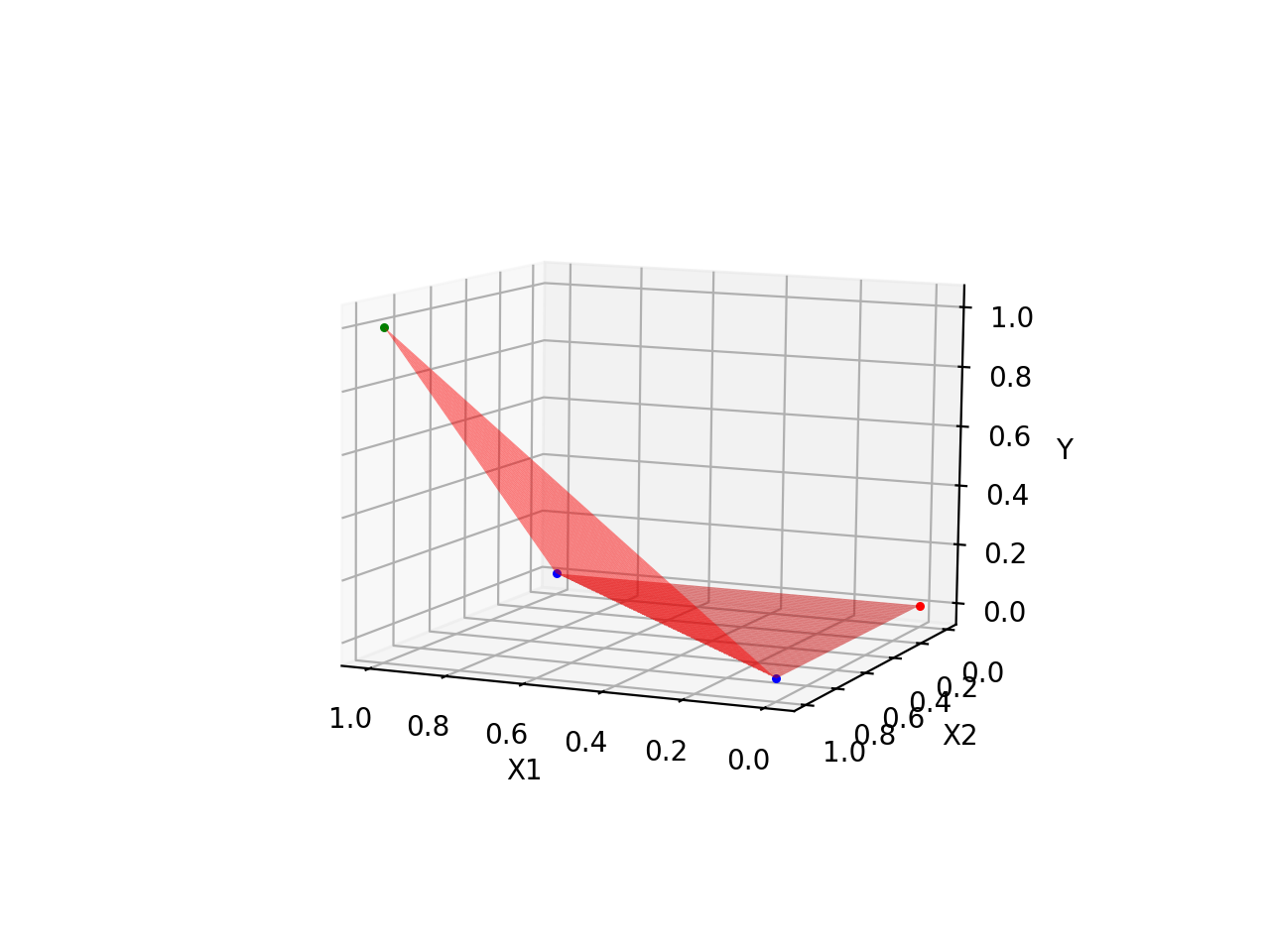 |
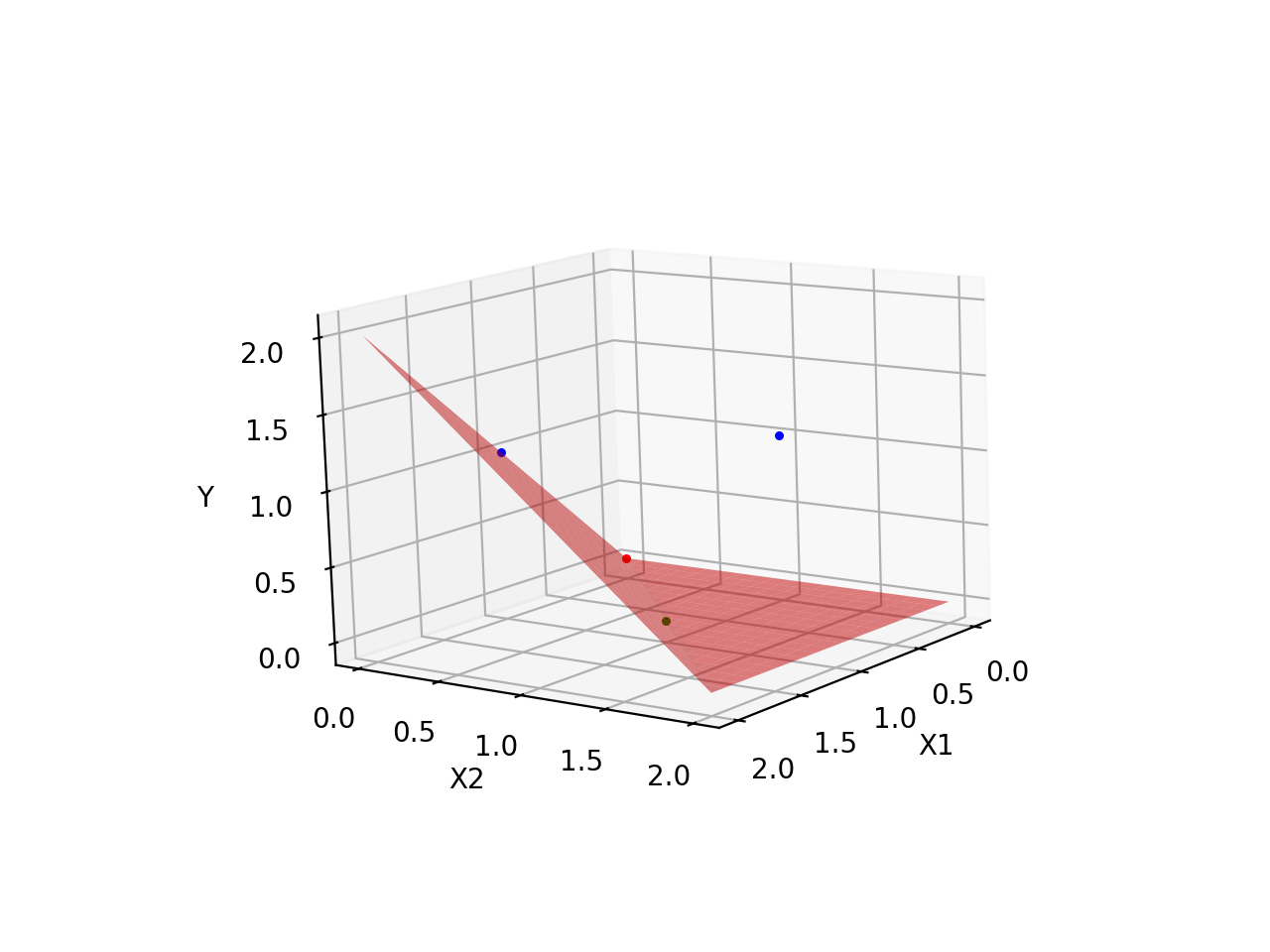 |
参考上述的平台特征,原来的方案:“貌似只能下面这么折叠(有个平面必须平行 x 轴),无法折叠出 V 字型的平面”
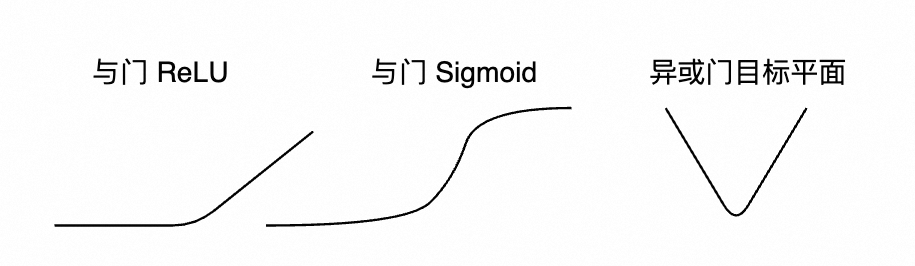
看上去很简单,把激活函数改成 $x^2$ 看似能很完美地解决这个问题,不过,激活函数需要具备下述特性(以下原因来自 AI 回复):
- 函数需单调,方向不一致,导致训练不稳定
- 函数为偶函数,是对称输出,无法区分正负
- 增长过快,容易梯度爆炸(直观理解,就是不好训练,权重、偏置可能训练了好几亿次,都没收敛)
那从输入着手呢,比如 ` y = sigmoid(w1 * x1 * x1 + w2 * x2 * x2 + b)` ,取得 x 的平方或 x 的三次方,会不会有更好的效果呢,答案是不会。
所以,需要另外的一种方式,让平台能够多折叠几次,最好是那种通用的,不管是什么函数,都有一个万能的模型来做相关预测,因为一开始模型具备是什么样子是不知道的,所以要有一个能模拟任何模型的函数。
好在这块领域,也有相关的理论支持,就是【通用近似定理/万能近似定理】[2],具体的表现就是多加一隐藏层。
神经网络
原有的与门模型定义:
\[\begin{aligned} h &= w_1 * x_1 + w_2 * x_2 + b \\ y &= ReLU(h) \end{aligned}\]按神经网络的思路,其定义可以可视化为如下表达方式,即:
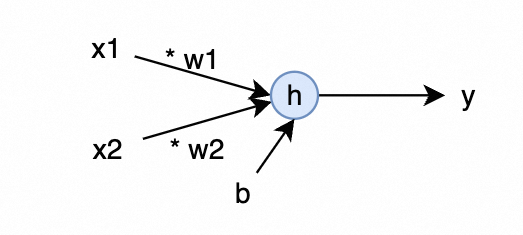
要解决原有与门模型「折叠次数」太少的问题,可以加一层 2 个神经元隐藏层的神经网络来解决,其表达方式如下:
中间层只加一个神经元行不行?答案是不行,这样本质上没有隐藏层的效果是一样的,只是单纯地在原有的 y 的基础上,再做了一次计算而已,所以,此处至少 2 个神经元(即 h1 和 h2)。
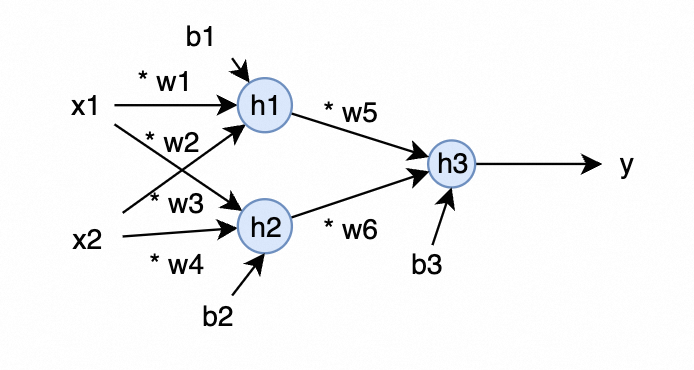
用数学表达方式就是下面这个样子(为方便起见,不涉及复杂导数计算,激活函数选用 ReLU )
\[\begin{aligned} h_1 &= w_1 * x_1 + w_3 * x_2 + b_1 \\ h_2 &= w_2 * x_1 + w_4 * x_2 + b_2 \\ y_1 &= ReLU(h_1) \\ y_2 &= ReLU(h_2) \\ h_3 &= w_5 * y_1 + w_6 * y_2 + b_3 \\ y &= ReLU(h_3) \end{aligned}\]为了先不引入「矩阵」的概念及其计算方法,此处特意用 $w_1 - w_6$ 及 $b_1 - b_3$ 来表示,并用纯算术计算来实现上述机器学习。因为笔者本人一开始学的时候,矩阵下标和各种矩阵计算,就能把人搞得晕头转向的。
所以,再次说明一下,矩阵只是为了更好地做表达、并行计算,可以先放一边,按最简单的、概念最少的思路,把整体流程捋一遍。
反向传播计算
这里最关键的是 w5 和 w6 怎么更新,所以,先对其求偏导,先提取跟 L 和 w5 有关的函数
\[\begin{aligned} L &= (y - \hat{y}) ^2 \\ y &= ReLU(h_3) \\ h_3 &= w_5 * y_1 + w_6 * y_2 + b_3 \\ \end{aligned}\]所以,w5 的偏导数有如下:
\[\begin{aligned} \frac{\partial L}{\partial w_5} &= \frac{\partial L}{\partial y} · \frac{\partial y}{\partial h_3} · \frac{\partial h_3}{\partial w_5}\\ &= \begin{cases} 2 * (y - \hat{y}) * 1 * y_1, & \text{if } h_3 > 0 \\ 2 * (y - \hat{y}) * 0 * y_1, & \text{otherwise} \end{cases} \\ &= \begin{cases} 2 * (y - \hat{y}) * y_1, & \text{if } h_3 > 0 \\ 0, & \text{otherwise} \end{cases} \end{aligned}\]对 w1 的偏导如下
\[\begin{aligned} L &= (y - \hat{y}) ^2 \\ y &= ReLU(h_3) \\ h_3 &= w_5 * y_1 + w_6 * y_2 + b_3 \\ y_1 &= ReLU(h1) \\ h_1 &= w_1 * x_1 + w_3 * x_2 + b_1 \\ \frac{\partial L}{\partial w_1} &= \frac{\partial L}{\partial y} · \frac{\partial y}{\partial h_3} · \frac{\partial h_3}{\partial y_1}· \frac{\partial y_1}{\partial h_1}· \frac{\partial h_1}{\partial w_1}\\ &= \begin{cases} 2 * (y - \hat{y}) * 1 * w_5 * 1 * x_1, & \text{if } h_3 > 0, & h_1 > 0 \\ 0, & \text{otherwise} \end{cases} \\ \end{aligned}\]Python 实现
由于随机初始化的问题,需要多运行几次(这可能就是算法为啥叫调参工程师的原因吧 ^-^ ),有时候会收敛到 y = 0.5 的平面
import random
# 学习率
rate = 0.01
# XOR 门测试数据
x = [[0, 0], [0, 1], [1, 0], [1, 1]]
y = [0, 1, 1, 0]
w1 = random.random()
w2 = random.random()
w3 = random.random()
w4 = random.random()
w5 = random.random()
w6 = random.random()
b1 = random.random()
b2 = random.random()
b3 = random.random()
# relu 激活函数
def relu(v):
if v < 0:
return 0
else:
return v
# 函数的定义
def h1(x1, x2):
return w1 * x1 + w3 * x2 + b1
def h2(x1, x2):
return w2 * x1 + w4 * x2 + b2
def h3(y1, y2):
return w5 * y1 + w6 * y2 + b3
def y1(h1):
return relu(h1)
def y2(h2):
return relu(h2)
print("初始化的权重和偏置: ")
print(w1, w2, w3, w4, w5, w6, b1, b2, b3)
# 训练迭代
epoch = 10000
while epoch > 0:
epoch = epoch - 1;
# w 和 b 更新算法
dw1 = dw2 = dw3 = dw4 = dw5 = dw6 = 0.0
db1 = db2 = db3 = 0.0
# 遍历测试数据集
for xs, yhat in zip(x, y):
[x1, x2] = xs
# 预测值
# 为区分函数和数值,所以新增 v 后缀
h1_v = h1(x1, x2)
h2_v = h2(x1, x2)
y1_v = relu(h1_v)
y2_v = relu(h2_v)
h3_v = h3(y1_v, y2_v)
y_v = relu(h3_v)
# w5 和 w6 更新
if h3_v > 0:
dw5 += 2 * (y_v - yhat) * y1_v
dw6 += 2 * (y_v - yhat) * y2_v
db3 += 2 * (y_v - yhat) * 1
if h1_v > 0:
dw1 += 2 * (y_v - yhat) * w5 * x1
dw3 += 2 * (y_v - yhat) * w5 * x2
db1 += 2 * (y_v - yhat) * w5
if h2_v > 0:
dw2 += 2 * (y_v - yhat) * w6 * x1
dw4 += 2 * (y_v - yhat) * w6 * x2
db2 += 2 * (y_v - yhat) * w6
dw1 = dw1 / len(x)
dw2 = dw2 / len(x)
dw3 = dw3 / len(x)
dw4 = dw4 / len(x)
dw5 = dw5 / len(x)
dw6 = dw6 / len(x)
db1 = db1 / len(x)
db2 = db2 / len(x)
db3 = db3 / len(x)
# 更新
w1 = w1 - rate * dw1
w2 = w2 - rate * dw2
w3 = w3 - rate * dw3
w4 = w4 - rate * dw4
w5 = w5 - rate * dw5
w6 = w6 - rate * dw6
b1 = b1 - rate * db1
b2 = b2 - rate * db2
b3 = b3 - rate * db3
print("训练后的权重和偏置: ")
print(w1, w2, w3, w4, w5, w6, b1, b2, b3)
def forword(x1, x2):
h1_v = h1(x1, x2)
h2_v = h2(x1, x2)
y1_v = relu(h1_v)
y2_v = relu(h2_v)
h3_v = h3(y1_v, y2_v)
y_v = relu(h3_v)
print(f"x1 {x1}, x2 {x2} => y1 {y1_v}, y2 {y2_v} => y {y_v}")
return y_v
print("预测结果:")
forword(0, 0)
forword(0, 1)
forword(1, 0)
forword(1, 1)
输出结果:
初始化的权重和偏置:
0.9550195641305104 0.14966699439564202 0.3724530186688523 0.2918470706407119 0.9307877788007731 0.15420500041785823 0.6885635070835702 0.007327282692478065 0.6720023468053917
训练后的权重和偏置:
0.9411855394820262 1.081520036084144 0.9411855383955807 1.0815200346093992 1.0624827954556706 -1.8492392682881917 0.10083647508443963 -1.0815200439276933 -0.10713294170194569
预测结果:
x1 0, x2 0 => y1 0.10083647508443963, y2 0 => y 4.0782296658048445e-06
x1 0, x2 1 => y1 1.0420220134800204, y2 0 => y 0.999997520106653
x1 1, x2 0 => y1 1.0420220145664658, y2 0 => y 0.9999975212609825
x1 1, x2 1 => y1 1.9832075529620468, y2 1.0815200267658498 => y 1.6602024642403679e-06
成功完成模型的训练后,可能得到的一个曲面如下:
| 成功拟合1 | 成功拟合2 |
|---|---|
 |
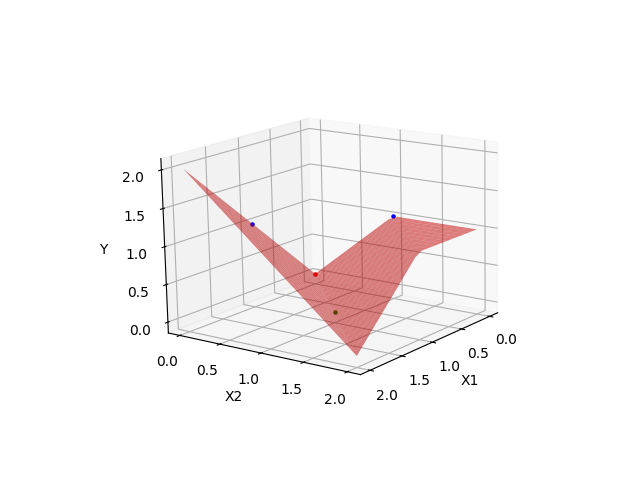 |
当然也有失败的,一开始折叠的方向错了,可能就落到局部最优,而不是全局最优,或者一开始就走了躺平路线的,所以,初始化很重要。
| 失败拟合1 | 失败拟合2 |
|---|---|
 |
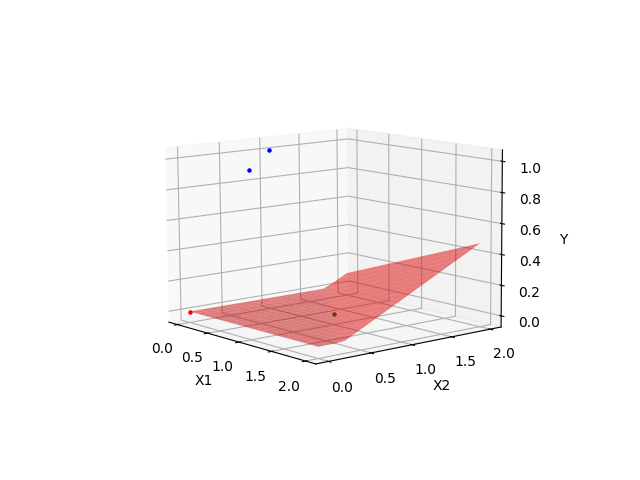 |
PyTorch 版本
import torch
import torch.nn as nn
# 测试数据
x = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]])
y = torch.tensor([[0.0], [1.0], [1.0], [0.0]])
# 创建预测模型,包含一个输入层(2个参数)、一个隐藏层(2个神经元)、一个输出,并在每个输出层添加一个 ReLU 激活函数
model = nn.Sequential(nn.Linear(2, 2), nn.ReLU(), nn.Linear(2, 1), nn.ReLU())
# 定义均方误差损失函数
mseloss = torch.nn.MSELoss()
# 随机梯度下降优化器
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 学习率为0.1, learning rate
# 执行梯度下降算法进行模型训练
for epoch in range(10000):
y_pred = model(x) # 计算预测值
loss = mseloss(y_pred, y) # 计算损失
optimizer.zero_grad() # 清零梯度
loss.backward() # 反向传播,计算梯度
optimizer.step() # 更新模型参数
# 预测
print(model.forward(torch.tensor([0.0, 0.0])))
print(model.forward(torch.tensor([0.0, 1.0])))
print(model.forward(torch.tensor([1.0, 0.0])))
print(model.forward(torch.tensor([1.0, 1.0])))
输出(同样要执行多次,有概率失败):
tensor([1.0848e-05], grad_fn=<ReluBackward0>)
tensor([1.0000], grad_fn=<ReluBackward0>)
tensor([1.0000], grad_fn=<ReluBackward0>)
tensor([1.0252e-05], grad_fn=<ReluBackward0>)
But, Why?
为什么加了中间层,有如此神奇的效果?
其实上述的权重,用矩阵的方式来描述,大致如下:
\[ReLU(\begin{bmatrix} w_1 & w_3 \\ w_2 & w_4 \end{bmatrix} \cdot \begin{matrix} x_1 \\ x_2 \end{matrix} + \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} ) = \begin{bmatrix} ReLU(w_1*x_1 + w_3*x_2 + b_1)\\ ReLU(w_2*x_1 + w_4*x_2 + b_2) \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \end{bmatrix}\]这里使用一种通过上述模型预测出的权重和偏置,能满足 xor 预测模型(此处有模型有多个解,这里取一种最简单的解法),即当权重和偏置取如下值的时候,损失为 0,能正常预测 xor 模型。
输入层到隐藏层的计算结果:
w1 = 1, w2 = 1, w3 = 1, w4 = 1, b1 = 0, b2 = -1
中间隐藏层到输出结果的计算如下:
w5 = 1, w6 = -2, b3 = 0
\(ReLU(\begin{bmatrix}
1 & -2 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
y_1 \\
y_2
\end{bmatrix}
+
\begin{bmatrix}
0
\end{bmatrix}
)
= 1 * y_1 -2 * y_2
= y\)
线形变换
用矩阵写的 w1-w4,从线形代数的角度看,就是线形变换。
此处的线形变换,可以简单理解为,用一种技术,对现有的二维坐标系做缩放、旋转、裁剪、翻转等操作,使得相关坐标点更容易拟合。
根据上述的预测模型,相关的二维坐标系变化如下:
- 横坐标为 x1,纵坐标为 x2
- 蓝色点表示预期输出为 0,红色竖线表示预期输出为 1
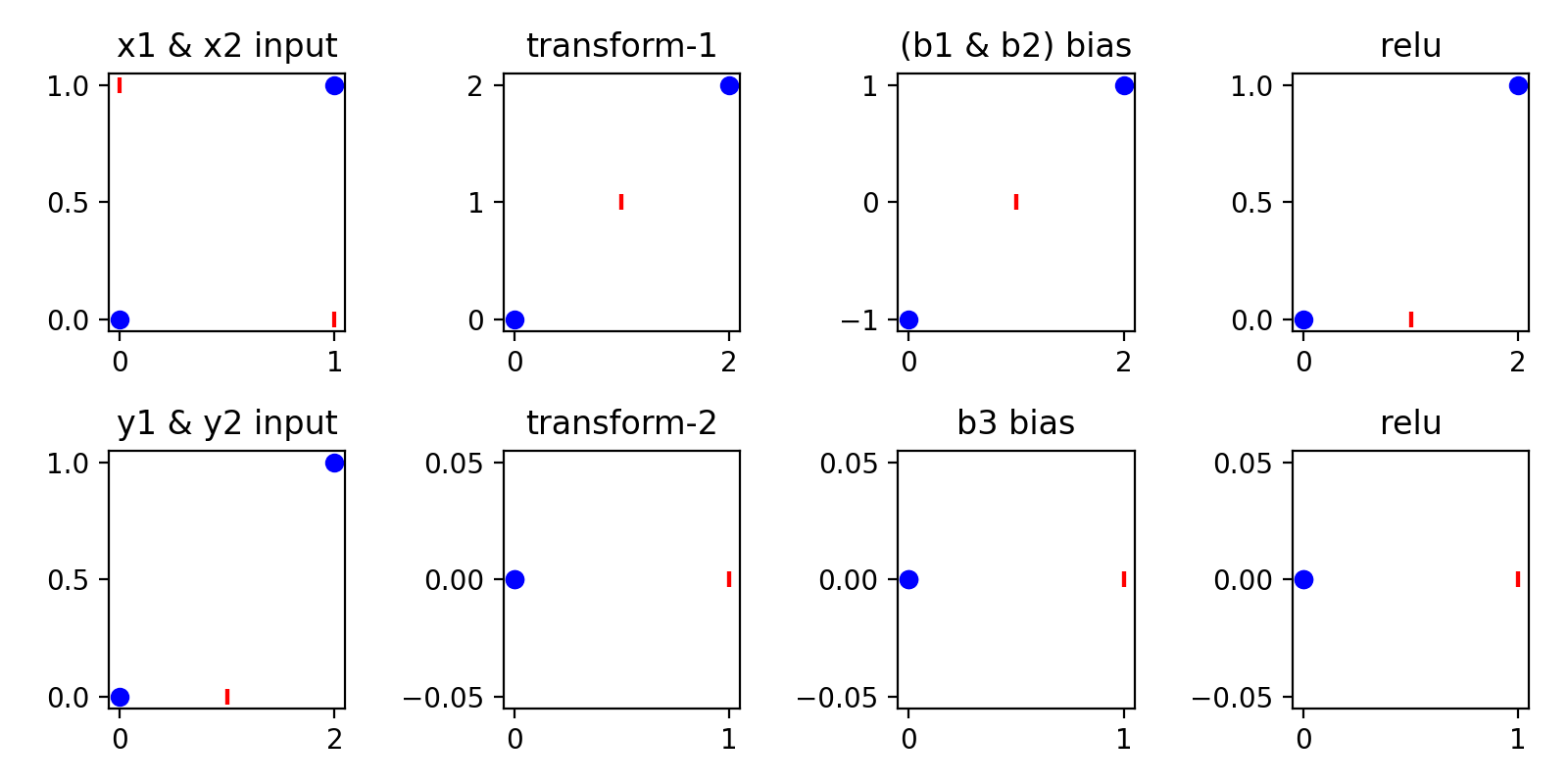
此处最为关键的是两次线性变换,即第一次的 transform-1
\[\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\]其变换之后,将 x1, x2 的原有 4 个点都压缩到一条 45 度的斜线上。然后通过 bias 和 relu,将其输出为 [0,0],[1,0],[2,1] 三个点。
类似如下这种,关于线性变换的更多内容,参考 3blue1brown 的线性代数的本质[3]:
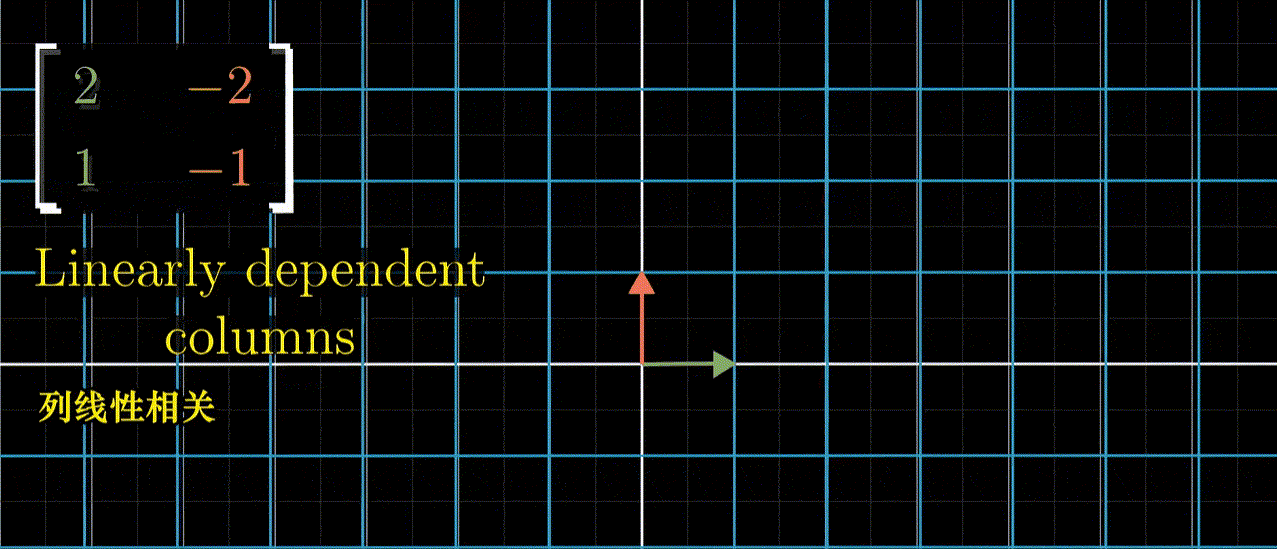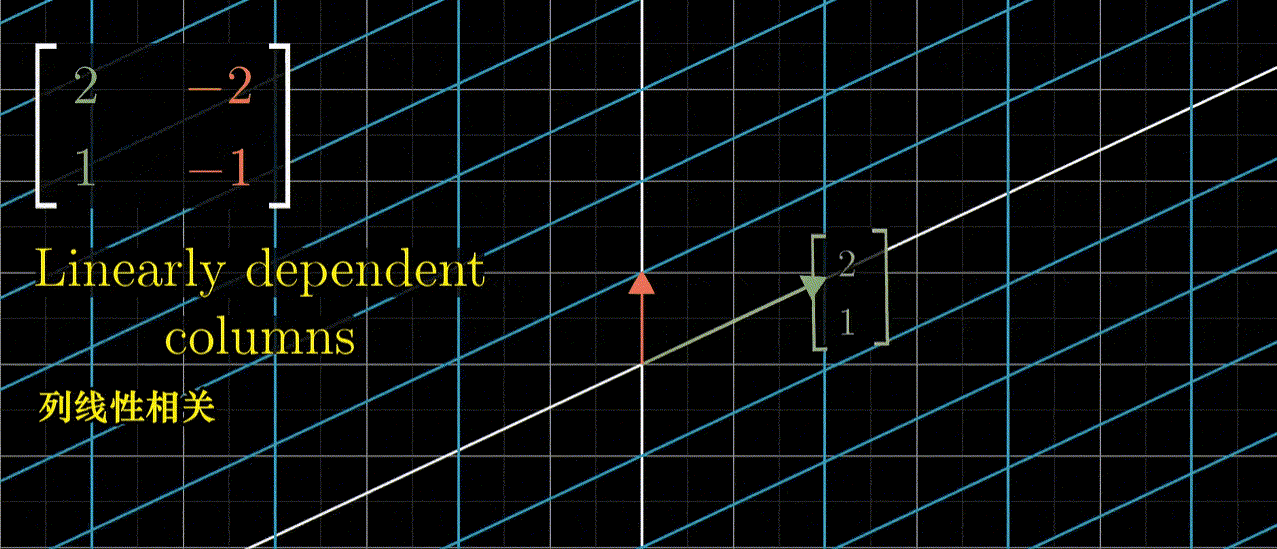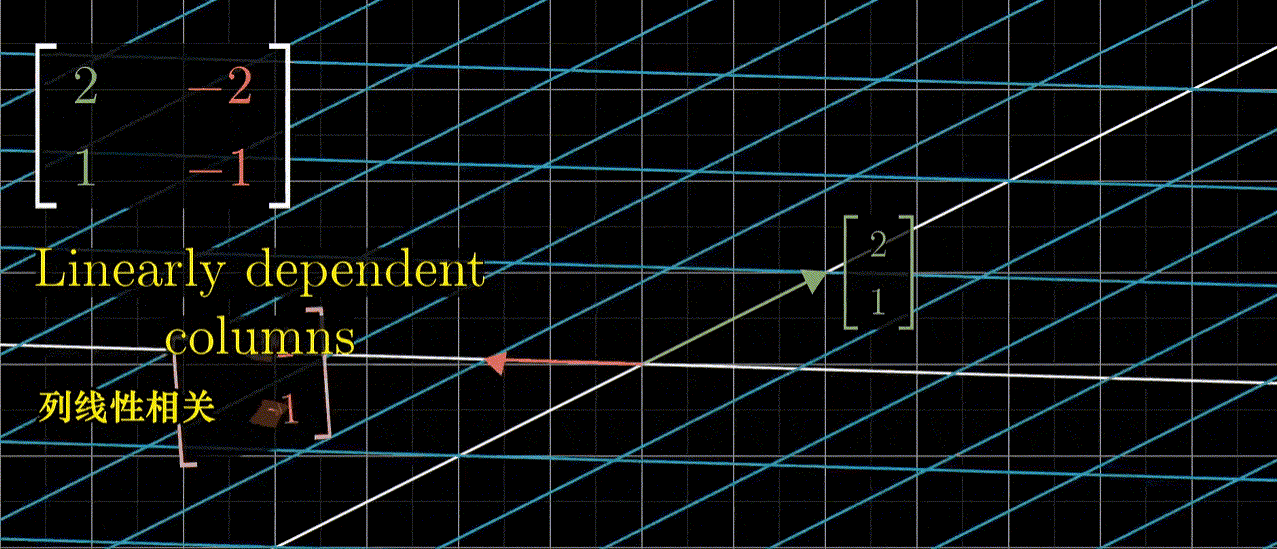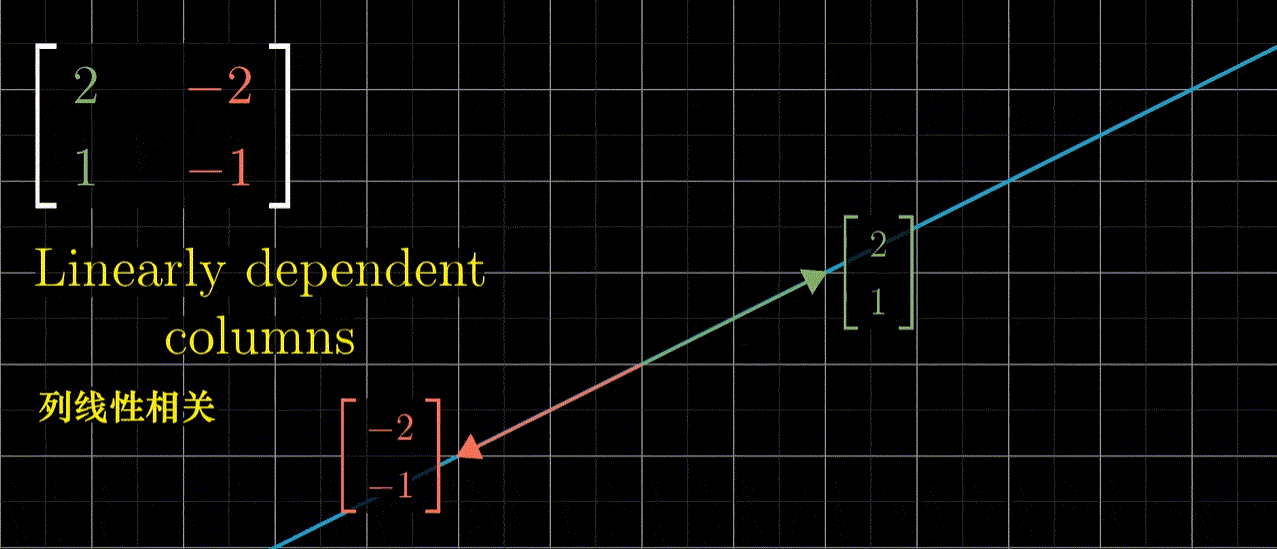
第二次的 transform-2,改成为二维的线性变换,即为
\[\begin{bmatrix} 1 & -2 \\ 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} y_1 \\ y_2 \end{bmatrix}\]其变换之后,将 [2, 1] 线形变换到 [0, 0],使得最终的点为 [0, 0], [1, 0]
相关系列
- 面向开发工程师的 0 基础机器学习教程 - 反向传播(一)最简单的机器学习算法,二维空间
- 面向开发工程师的 0 基础机器学习教程 - 激活函数(二)最简单的机器学习算法,三维空间
- 面向开发工程师的 0 基础机器学习教程 - 神经网络(三)最简单的机器学习算法,神经网络
限于本人学识与能力,文中难免存在疏漏与不足之处,恳请读者不吝指正。