面向开发工程师的 0 基础机器学习教程 - 反向传播（一）

本文采用最简单的模型 y = ax + b 为例，通过两个测试数据，做一个最简单机器学习算法，通过多次训练，完成模型迭代，最终来预测第三个数据的值。相当于机器学习界的《hello world！》

基本概念

Q: 为什么需要机器学习？

A: 机器学习是对传统简单、线性的逻辑处理的补充，比如：手写数字、图像识别等，有大量变量，且无法用明确的规则或逻辑来处理。一个例子：你不能用对每个像素的 if / else 判断，来识别出某张图片的数字是 3 等，或者逻辑写起来比较复杂。

Q: 什么是机器学习？

A: 机器学习的本质，就是通过有限的已知数据，来做模型的训练，来预测未知数据。

机器学习

接下来，用一个及其简单的例子，来介绍机器学习：

假设知道了一些有限的输入和输出，比如：输入为 1，输出为 6；输入为 2，输出为 8。
然后通过这些已有的数据，来训练一个模型。
训练完成后，预测一些未知的输入，比如：输入为 3，输出为什么？

模型定义：

因为只有一个输入和一个输出，所以，可以构建函数来预测这个模型，比如：y = ax + b

训练模型：

随机初始化模型参数，假设：a = 4, b = 1
模型初始化为 y = 4 * x + 1
通过测试数据来训练模型：
1. 输入为 1 时，模型输出为 5，数据实际值为 6，误差有 5 - 6 = -1
2. 输入为 2 时，模型输出为 9，数据实际值为 8，误差有 9 - 8 = 1
误差计算，因为输出数据中，有些大有些小，为了误差不被正负相抵消，所以将每次误差平方再相加来计算总误差。
1. 输入 1 的误差为 (5 - 6) * (5 - 6) = -1 * (-1) = 1
2. 输入 2 时误差为 (9 - 8) * (9 - 8) = 1 * 1 = 1
基于误差，更新模型参数 a 和 b：
1. a 更新
  1. 定义更新大小：2 * (模型预测值 - 真实值) * x （此处涉及导数，最为核心的内容，后续介绍解释）
  2. 计算所有测试输入的误差 2 * (5 - 6) * 1 + 2 * (9 - 8) * 2 = 2 然后平均 = 误差值 / 测试数据量 = 2 / 2 = 1
  3. a = a - 0.1 * 1 = 3.9 (为了避免一下子减太多，每次更新参数时，乘以一个系数，慢慢变化，此处我们定义了 0.1)
2. b 更新
  1. 定义更新大小：2 * (模型预测值 - 真实值) * 1 （注意此处没有 x，因为更新的是 b，从导数视角，和 x 没有关系）
  2. 计算所有更新值：2 * (5 - 6) + 2 * (9 - 8) = 0 然后平均 = 误差值 / 测试数据量 = 0 / 2 = 0
  3. b = b - 0.1 * 0 = 1
循环训练【3、4、5、6】步骤，直到误差小于某个阈值，或者训练次数达到某个值。实际运行后，a 会趋近为 2，b 会趋近为 4
模型训练完成，预测模型会趋近于定义：y = 2x + 4
预测未知数据：y = 2 * 3 + 4 = 10，所以输入 3 的预测值为 10

上述就是机器学习的核心步骤，除了【更新函数】的定义没做相关解释外，如果能看懂，那么就已基本理解机器学习的核心概念。

下面先用代码简单实现一下，以开发工程师的视角，用程序来训练并预测一下 3 的输出是多少。

机器学习之 JS 版本

记住，机器学习的核心内容就这些，不要有畏惧心理。再怎么复杂，再怎么高深的数学公式，在开发工程师的视角，完成训练、预测，就下述不到 50 行的代码，核心代码就 10 行不到。

// 随机初始化
let a = 4,
  b = 1;

// 学习率
const rate = 0.1;

// 测试数据
const data = [
  [1, 6],
  [2, 8],
];

// 预测函数
const predict = (x) => a * x + b;

// 模型训练 1000 次
let epoch = 1000;
while (epoch--) {

  // 计算更新值
  let deltaA = 0;
  let deltaB = 0;
  // 循环测试数据
  data.forEach(([x, y]) => {
    deltaA += 2 * (predict(x) - y) * x;
    deltaB += 2 * (predict(x) - y) * 1;
  });
  deltaA = deltaA / data.length;
  deltaB = deltaB / data.length;

  // 更新
  a = a - rate * deltaA;
  b = b - rate * deltaB;
}

// 完成模型训练
console.log(`y = ${a}x + ${b}`);
// 输出：
// y = 2.00000078438591x + 3.9999987308369374

// 预测模型为 y = 2x + 4;
// 推理 3 的输出，预测结果为：x = 3, y = 10
console.log(`x = 3, y = ${predict(3)}`);
// 输出：
// x = 3, y = 10.000001083994668

机器学习之 Java 版本

为了方便前后端大部分的开发工程师，还写了 Java 版本，但后续的样例代码，都会尽可能使用 python，毕竟机器学习框架，python 生态最有优势。此处仅为了降低大家的认知门槛。

public class Main {

    // 随机初始化
    public static double a = 4, b = 1;

    // 学习率
    public static double rate = 0.1;

    // 测试数据集
    public static double[][] data = {
            {1, 6},
            {2, 8}
    };

    // 预测函数
    public static  double predict(double x) {
        return a * x + b;
    }

    public static void main(String[] args) {

        // 训练模型
        int epoch = 1000;
        while (--epoch > 0) {

            // 计算更新值
            double deltaA = 0;
            double deltaB = 0;
            // 循环测试数据
            for (double[] doubles: data) {
                double x = doubles[0], y = doubles[1];
                deltaA += 2 * (predict(x) - y) * x;
                deltaB += 2 * (predict(x) - y) * 1;
            };
            deltaA = deltaA / data.length;
            deltaB = deltaB / data.length;

            // 更新
            a = a - rate * deltaA;
            b = b - rate * deltaB;
        }

        // 完成模型训练
        System.out.println("y = " + a + "x + " + b);
        // 输出
        // y = 2.0000007959993846x + 3.999998712045941

        // 预测模型为 y = 2x + 4;
        // 推理 3 的输出，预测结果为：x = 3, y = 10
        System.out.println("x = 3, y = " + predict(3));
        // 输出
        // x = 3, y = 10.000001100044095
    }
}

误差计算

为了计算预测模型和实际模型的差距，误差计算一般采用欧几里得距离（又称欧式距离），其几何意义就是在二维坐标系中的两个点的距离，其定义如下：

\[d(p, q) = \sqrt{(q_1 - p_1) ^ 2 + (q_2 - p_2) ^ 2} \\ d(p, q) ^ 2 = (q_1 - p_1) ^ 2 + (q_2 - p_2) ^ 2\]

为方便起见，在机器学习中一般用欧式距离平方来计算

应用在当前预测模型和机器学习中，即图中红色点与紫色点的距离总和 [8]

测试数据为 (1, 6), (2, 8)，图中红色的点
当前的预测模型 a = 4, b = 1，即 y = 4x + 1 为蓝色直线
通过模型预测的值为 (1, 5), (2, 9)，图中紫色的点

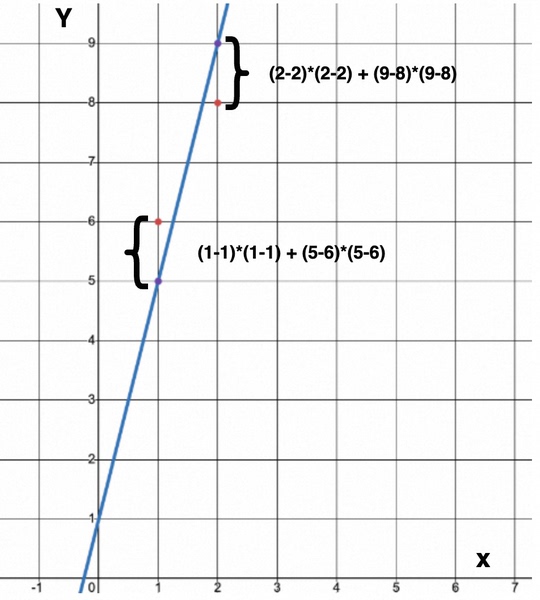
其误差，按输入和输出的欧式距离的平方来算，两次测试输入输出的欧式距离总和即为：

\[\begin{align} (欧式距离) ^ 2 的误差总和 &= (x 为 1 的欧式距离) ^ 2 + (x 为 2 的欧式距离) ^ 2 \\ &= [(x_1 - x_1) * (x_1 - x_1) + (4 * x_1 + 1 - 6) * (4 * x_1 + 1 - 6)] + [(x_2 - x_2) * (x_2 - x_2) + (4 * x_2 + 1 - 8) * (4 * x_2 + 1 - 8)] \\ &= [(1 - 1) * (1 - 1) + (5 - 6) * (5 - 6)] + [(2 - 2) * (2 - 2) + (9 - 8) * (9 - 8)] \\ &= (0 + 1) + (0 + 1) \\ &= 2 \end{align}\]

机器学习的训练

机器学习训练过程中，其本质，就是如何将误差降低到最小。相关定义如下，其误差函数在机器学习中也叫 loss 损失函数

\[\begin{align} Loss 损失函数 &= (ax + b - y) ^ 2 \\ \end{align}\]

接下来，为方便表达，将结合机器学习的相关概念，来说明如何使用「反向传播」，通过一次次的训练，将其误差降低到最小。

反向传播

反向传播，比较主观的解释就是根据误差的大小，将不同的权重和偏置做更新

误差大的，更新的幅度也应该大，所以这个更新的大小和误差有关（即 loss 函数的值）
权重大的，更新的幅度也应该大（如：a 与 b 相比，a 由于和 x 乘了一下，所以一开始，a 的更新幅度，体感上应该比 b 更大一些）

这个更新幅度，其实就是数学意义上的导数[5]，即在当前点的斜率。又因为模型定义有多个变量，所以，需要对函数求偏导数。

因此，反向传播及梯度下降的本质，就是根据损失误差，对 a 和 b 分别求偏导数，然后根据偏导数的数据，来更新对应的值。这便是机器学习算法的核心。

此处开始涉及少量数学公式，已筛选和截取了尽可能少的数学内容，但都是必须的，核心就在偏导数的理解和计算上。可以先理解个大概，慢慢消化。

导数

导数：函数在某一点的导数是指这个函数在这一点附近的变化率（即函数在这一点的切线斜率）

常见的求导函数[7]：

\[\begin{aligned} (c)' &= 0; \\ (x^a)' &= ax^{a-1} \hspace{1em} (a \in R); \end{aligned}\]

就上面的两个求导函数，本文档已经够用了：

常量的导数为 0，比如： $(3)’ = 0$
指数函数，比如： $(x^3)’ = 3x^2$

偏导数

偏导数：一个多变量的函数（或称多元函数），对其中一个变量（导数）微分，而保持其他变量恒定

其他变量恒定，可以直接当成常量看待

求模型定义中的偏导数[4]

\[\begin{aligned} y &= ax + b \\ \Rightarrow \frac{\partial y}{\partial a} &= 1 · a ^ 0 · x + 0 = x \text{\hspace{1em}对 a 求偏导数} \\ \Rightarrow \frac{\partial y}{\partial b} &= 0 + 1 · b ^ 0 = 1 \text{\hspace{1em}对 b 求偏导数} \\ \end{aligned}\]

求损失函数偏导数

\[\begin{aligned} L &= (y - \hat{y})^2 \\ &= y^2 - 2y\hat{y} + \hat{y}^2\\ \Rightarrow \frac{\partial L}{\partial y} &= 2y - 2\hat{y} + 0 \\ &= 2(y - \hat{y}) \end{aligned}\]

$y$ 为模型输出值
$\hat{y}$ 为测试实际值

更新权重 a

我们希望根据测试数据来更新 a 的值，目标是使得 loss 的值尽可能的小，这样就和正确的模型尽可能近似了。

所以为了求出如何更新 a，此处需要对（目标函数） L 对 a 求偏导数，这样就能知道 a 应该是变大还是变小（正负值），以及应该变多少（偏导数的斜率）。

直接求偏导

为避免引入其他更多的数学概念，使用最直接的方式来求偏导

\[\begin{aligned} y &= ax + b \\ L &= (y - \hat{y})^2 \\ &= (ax + b - \hat{y})(ax + b - \hat{y}) \\ &= a^2x^2 + axb - ax\hat{y} + bax + b^2 - b\hat{y} - \hat{y}ax - \hat{y}b + \hat{y}^2 \\ \therefore \frac{\partial L}{\partial a} &= 2ax^2 + bx - x\hat{y} + bx + 0 - 0 - \hat{y}x - 0 + 0 \\ &= 2ax^2 + 2bx - 2x\hat{y} \\ &= 2(ax + b - \hat{y})x \\ &= 2(y - \hat{y})x \end{aligned}\]

链式法则求偏导

\[\begin{aligned} L &= (y - \hat{y}) ^ 2\\ y &= ax + b \\ \because\quad &\frac{\partial L}{\partial a} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial a} \text{\hspace{2em}(链式法则)}\\ \because\quad &\frac{\partial L}{\partial y} = 2(y - \hat{y}),\quad \frac{\partial y}{\partial a} = x \\ \therefore\quad &\frac{\partial L}{\partial a} = 2(y - \hat{y}) \cdot x \end{aligned}\]

此处对复合函数的求导，用的是链式法则[3]，很多数学证明，可以直接拿过来用，此处对于开发工程师来说，可以「不求甚解」些。

当然可以发现，用链式法则求出的偏导，跟直接求出的偏导的结果是一致的。

更新逻辑

所以程序中更新 a 就是 deltaA += 2 * (predict(x) - y) * x;

假设学习率 $\eta$ 为 0.1，则对 a 的更新定义如下：

\[\begin{aligned} a &\leftarrow a - \eta \cdot \frac{\partial L}{\partial a} \\ a &\leftarrow a - \eta \cdot (\sum_{i=1}^{n} 2(y_i - \hat{y_i}) \cdot x_i)/n \\ a &\leftarrow 4 - 0.1 \cdot [2 * (5 - 6) * 1 + 2 * (9 - 8) * 2] / 2 \\ &= 4 -0.1 \\ &= 3.9 \end{aligned}\]

误差需要乘 x，这是区别 b 最显著的特点，也给人 a 的更新幅度应该更大的感觉（也就是一开始他的下降更大一些）

更新偏置 b

同理，为了知道如何更新 b（正负值及斜率），求 L 函数对 b 的偏导数

\[\begin{aligned} \because\quad &\frac{\partial L}{\partial b} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial b} \text{\hspace{2em}(链式法则)}\\ \because\quad &\frac{\partial L}{\partial y} = 2(y - \hat{y}),\quad \frac{\partial y}{\partial b} = 1 \\ \therefore\quad &\frac{\partial L}{\partial b} = 2(y - \hat{y}) \cdot 1 \end{aligned}\]

所以程序中更新 b 就是 deltaB += 2 * (predict(x) - y) * 1;

假设学习率 $\eta$ 为 0.1，则

\[\begin{aligned} a &\leftarrow a - \eta \cdot \frac{\partial L}{\partial b} \\ a &\leftarrow a - \eta \cdot (\sum_{i=1}^{n} 2(y_i - \hat{y_i}) \cdot 1)/n \\ a &\leftarrow 4 - 0.1 \cdot [2 * (5 - 6) * 1 + 2 * (9 - 8) * 1] / 2 \\ &= 1 - 0 \\ &= 1 \end{aligned}\]

备注：第一次训练迭代 b 不做更新，只有 a 更新了，第二次训练迭代，随着 a 的变化，b 也会做相关更新，可以对程序代码中打印出每次 a 和 b 的值，做一些观察和验证。

至此，样例中的所有步骤，均已解释完毕。

机器学习之 Python 版本

为了方便使用 python 生态的机器学习框架，写了一个 python 版本的基础版与 pytorch 版本，方便学习与做对比。

基础版本

参考之前的 JS / Java 版本，翻译成 python 如下：

# 随机初始值
a = 4.0
b = 1.0

# 学习率 learning rate
rate = 0.1
data = [
    [1, 6],
    [2, 8]
]

# 预测模型
def predict(x):
    return a * x + b

# 迭代次数
epoch = 1000
while epoch > 0:
    epoch = epoch - 1;
    
    # 变化计算
    deltaA = 0
    deltaB = 0
    # 循环测试数据
    for doubles in data:
        [x, y] = doubles
        deltaA += 2 * (predict(x) - y) * x
        deltaB += 2 * (predict(x) - y) * 1
    deltaA = deltaA / len(data)
    deltaB = deltaB / len(data)

    # 更新
    a = a - rate * deltaA
    b = b - rate * deltaB

# 预测模型
print("y = " + str(a) + "x" + " + " + str(b))

# 预测值，推理 3 的输出
print("x = 3, y = " + str(predict(3)))

输出（符合预期）

y = 2.00000078438591x + 3.9999987308369374
x = 3, y = 10.000001083994668

pytorch 进阶版本

使用 torch 框架[6]，快速实现上述机器学习

import torch
import torch.nn as nn

# 测试数据
x = torch.tensor([[1.0], [2.0]])
y = torch.tensor([[6.0], [8.0]])

# 创建预测模型，包含线性层，一个输入、一个输出
model = nn.Sequential(nn.Linear(1, 1))

# 定义均方误差损失函数
mseloss = torch.nn.MSELoss()
# 随机梯度下降优化器
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)  # 学习率为0.1， learning rate

# 执行梯度下降算法进行模型训练
for epoch in range(1000):
    y_pred = model(x)  # 计算预测值
    loss = mseloss(y_pred, y)  # 计算损失
    
    optimizer.zero_grad()  # 清零梯度
    loss.backward()  # 反向传播，计算梯度
    optimizer.step()  # 更新模型参数

# 打印模型
for layer in model.children():
    if isinstance(layer, nn.Linear):
        print("权重（就是样例中的 a）" + str(layer.state_dict()['weight'][0].item()))
        print("偏置（就是样例中的 b）" + str(layer.state_dict()['bias'][0].item()))

# 推理 3 的输出
print(model.forward(torch.tensor([3.0])).item())

最终输出：

权重（就是样例中的 a）2.0000054836273193
偏置（就是样例中的 b）3.9999914169311523
10.000007629394531

参考

反向传播的推导可以借助 AI 来理解，prompt 为：最简单的反向传播，一个输入，一个输出，y=ax+b，如何反向传播
playground.tensorflow
链式法则
偏导数
导数
PyTorch 第一个神经网络
常见函数求导公式
在线画图表