从 RNN 到 Attention
RNN 到 LSTM/GRU 到 seq2seq 到 Attention 的代码实践(个人记录)。
RNN
通过对 神经网络 的基础学习,就可以稍微深入学习一下 RNN 了,选 RNN,是因为 Transformer 是现代 LLM 大语言模型的基础,沿着 Transformer 往上追溯,就可以看到 Sequence-to-sequence,然后是 LSTM 和 RNN。
RNN(Recurrent Neural Networks)循环神经网络是一类神经网络架构,专门用于处理序列数据,能够捕捉时间序列或有序数据的动态信息,能够处理序列数据,如文本、时间序列或音频。
RNN 例子
参考 A friendly introduction to Recurrent Neural Networks
一个简单的 RNN:
你有一个非常喜欢烹饪的室友,他每天都烹饪一道食品,并遵循一个固定的规律:苹果派 -> 汉堡 -> 鸡肉 -> 苹果派 -> 汉堡 -> 鸡肉 -> 苹果派…,以此循环,当天的食物,取决于前一天的食物,这便形成了一个时间序列上的依赖关系。
带有外部输入的 RNN
烹饪规则:室友今天的食物,取决
前一天的做的食物和今天的天气,如果是晴天,他会选择不做新食物,和昨天一样;如果是雨天,他会选择做序列中的下一道菜。
这里的例子便构成了 RNN 最基础的概念。
RNN 实现
通过上述例子,烹饪规则就是 RNN 的隐藏状态(即苹果派 -> 汉堡 -> 鸡肉的这个循环),天气就是 RNN 的外部输入。其中第 t 天的隐藏状态记为 $h_t$,$x$ 为天气。
所以,要求第 t 天的食物,有如下公式:
\[h_t = \tanh\left( \mathbf{W}_{hh} \mathbf{h}_{t-1} + \mathbf{W}_{xh} \mathbf{x}_t + \mathbf{b}_h \right)\]用图片做相关展示,如下:
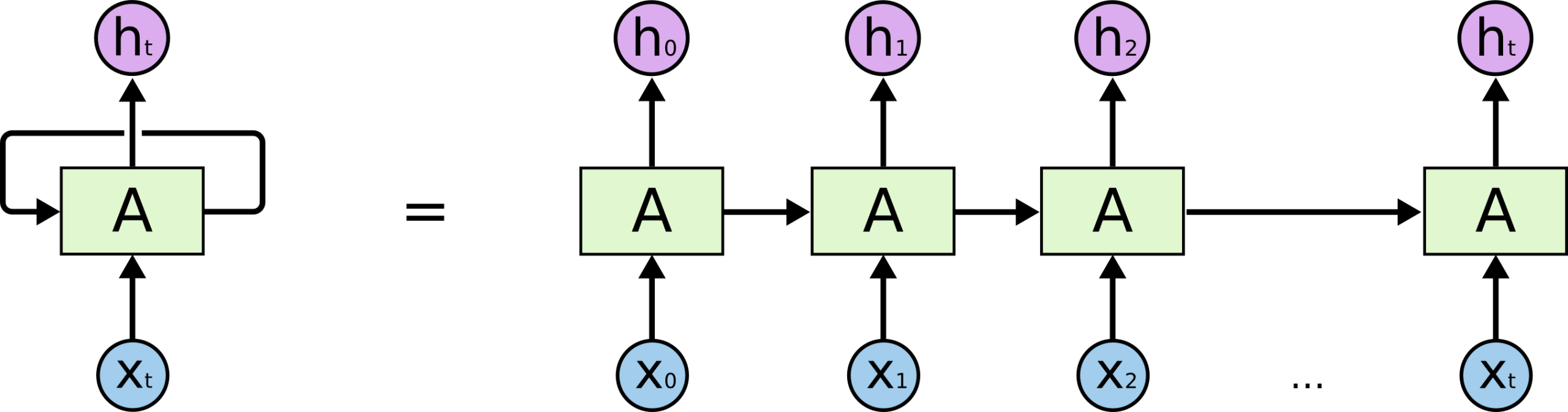
参考 recurrent-neural-network,相关实现代码也比较简单,如下:
class SimpleRNN(nn.Module):
def __init__(self):
super().__init__()
# RNN 的权重矩阵
self.W_xh = nn.Parameter(torch.randn(hidden_size, input_size)) # 输入权重
self.W_hh = nn.Parameter(torch.randn(hidden_size, hidden_size)) # 隐藏状态权重
self.b_h = nn.Parameter(torch.zeros(hidden_size, 1)) # 偏置项
# 输出层
self.out = nn.Sequential(
nn.Linear(hidden_size, output_size),
nn.Sigmoid()
)
def forward(self, x, hidden):
hidden_next = torch.tanh(self.W_hh @ hidden + self.W_xh @ x + self.b_h)
return self.out(hidden_next.T), hidden_next
随着实践的深入,你会发现,不管你在输入、输出怎么调整神经网络的层级、参数等等,都无法完成例子中「关于天气的烹饪规则」,归根结底是这样的模型,过于简单,甚至都无法习得仅有一个外部输入(天气)的烹饪规则循环。
所以,LSTM 和 GRU 出场了。
LSTM
LSTM(Long Short-Term Memory) 是 RNN 的一种改进架构,专门设计来解决标准 RNN 的长期依赖问题。
相关数学定义如下:
\[\begin{aligned} f_t &= \sigma\left( W_f x_t + U_f h_{t-1} + b_f \right) & \text{(forget gate)} \\ i_t &= \sigma\left( W_i x_t + U_i h_{t-1} + b_i \right) & \text{(input gate)} \\ \tilde{c}_t &= \tanh\left( W_c x_t + U_c h_{t-1} + b_c \right) & \text{(candidate cell state)} \\ c_t &= f_t \odot c_{t-1} + i_t \odot \tilde{c}_t & \text{(cell state update)} \\ o_t &= \sigma\left( W_o x_t + U_o h_{t-1} + b_o \right) & \text{(output gate)} \\ h_t &= o_t \odot \tanh(c_t) & \text{(hidden state)} \end{aligned}\]- $x_t \in \mathbb{R}^{d}$:时刻 $t$ 的输入向量
- $h_t \in \mathbb{R}^{h}$:时刻 $t$ 的隐藏状态(输出)
- $c_t \in \mathbb{R}^{h}$:时刻 $t$ 的细胞状态(cell state)
- $\sigma(\cdot)$:Sigmoid 激活函数(值域 $[0, 1]$)
- $\tanh(\cdot)$:双曲正切函数(值域 $[-1, 1]$)
- $\odot$:Hadamard 积(逐元素相乘)
- $W_* \in \mathbb{R}^{h \times d}$:输入到门的权重矩阵
- $U_* \in \mathbb{R}^{h \times h}$:隐藏状态到门的权重矩阵
- $b_* \in \mathbb{R}^{h}$:偏置向量

在不使用 torch 自带的 RNN 库的情况下,相关代码如下:
class LSTMRNN(nn.Module):
def __init__(self):
super(LSTMRNN, self).__init__()
# https://en.wikipedia.org/wiki/Long_short-term_memory
# LSTM 的权重矩阵
# 输入门
self.W_f = nn.Parameter(torch.randn(hidden_size, input_size))
self.U_f = nn.Parameter(torch.randn(hidden_size, hidden_size))
self.b_f = nn.Parameter(torch.zeros(hidden_size, 1))
# 遗忘门
self.W_i = nn.Parameter(torch.randn(hidden_size, input_size))
self.U_i = nn.Parameter(torch.randn(hidden_size, hidden_size))
self.b_i = nn.Parameter(torch.zeros(hidden_size, 1))
# 输出门
self.W_o = nn.Parameter(torch.randn(hidden_size, input_size))
self.U_o = nn.Parameter(torch.randn(hidden_size, hidden_size))
self.b_o = nn.Parameter(torch.zeros(hidden_size, 1))
# 候选记忆单元
self.W_c = nn.Parameter(torch.randn(hidden_size, input_size))
self.U_c = nn.Parameter(torch.randn(hidden_size, hidden_size))
self.b_c = nn.Parameter(torch.zeros(hidden_size, 1))
# 输出层
self.o_y = nn.Sequential(
nn.Linear(hidden_size, output_size),
nn.Sigmoid()
)
def forward(self, x, state):
# state: (h_prev, c_prev)
h_prev, c_prev = state
# 输入门
f = torch.sigmoid(self.W_f @ x + self.U_f @ h_prev + self.b_f)
# 遗忘门
i = torch.sigmoid(self.W_i @ x + self.U_i @ h_prev + self.b_i)
# 输出门
o = torch.sigmoid(self.W_o @ x + self.U_o @ h_prev + self.b_o)
# 候选记忆单元
c_tilde = torch.tanh(self.W_c @ x + self.U_c @ h_prev + self.b_c)
# 新的 cell 状态
c_next = f * c_prev + i * c_tilde
# 新的 hidden 状态
h_next = o * torch.tanh(c_next)
# 输出层
y = self.o_y(h_next.T)
return y.T, (h_next, c_next)
GRU
LSTM 的缺点是参数过多,不容易训练,所以又出了一个:Gated recurrent unit 参数更少,更易训练。
相关的数学定义如下:
\[\begin{aligned} z_t &= \sigma\left( W_z x_t + U_z h_{t-1} + b_z \right) & \text{(update gate)} \\ r_t &= \sigma\left( W_r x_t + U_r h_{t-1} + b_r \right) & \text{(reset gate)} \\ \tilde{h}_t &= \tanh\left( W_h x_t + U_h (r_t \odot h_{t-1}) + b_h \right) & \text{(candidate hidden state)} \\ h_t &= (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t & \text{(final hidden state)} \end{aligned}\]| 符号 | 含义 |
|---|---|
| $x_t \in \mathbb{R}^{d}$ | 时刻 $t$ 的输入向量 |
| $h_t \in \mathbb{R}^{h}$ | 时刻 $t$ 的隐藏状态(GRU 的输出) |
| $z_t \in \mathbb{R}^{h}$ | 更新门(update gate):控制保留多少历史信息 vs 使用新候选状态 |
| $r_t \in \mathbb{R}^{h}$ | 重置门(reset gate):控制忽略多少历史信息来计算候选状态 |
| $\tilde{h}_t \in \mathbb{R}^{h}$ | 候选隐藏状态 |
| $\sigma(\cdot) $ | Sigmoid 激活函数(输出范围 $[0, 1]$) |
| $\tanh(\cdot) $ | 双曲正切函数(输出范围 $[-1, 1]$) |
| $\odot $ | Hadamard 积(逐元素相乘) |
| $W_, U_ \in \mathbb{R}^{h \times d}, \mathbb{R}^{h \times h}$ | 权重矩阵 |
| $b_* \in \mathbb{R}^{h}$ | 偏置向量 |
示意图如下:
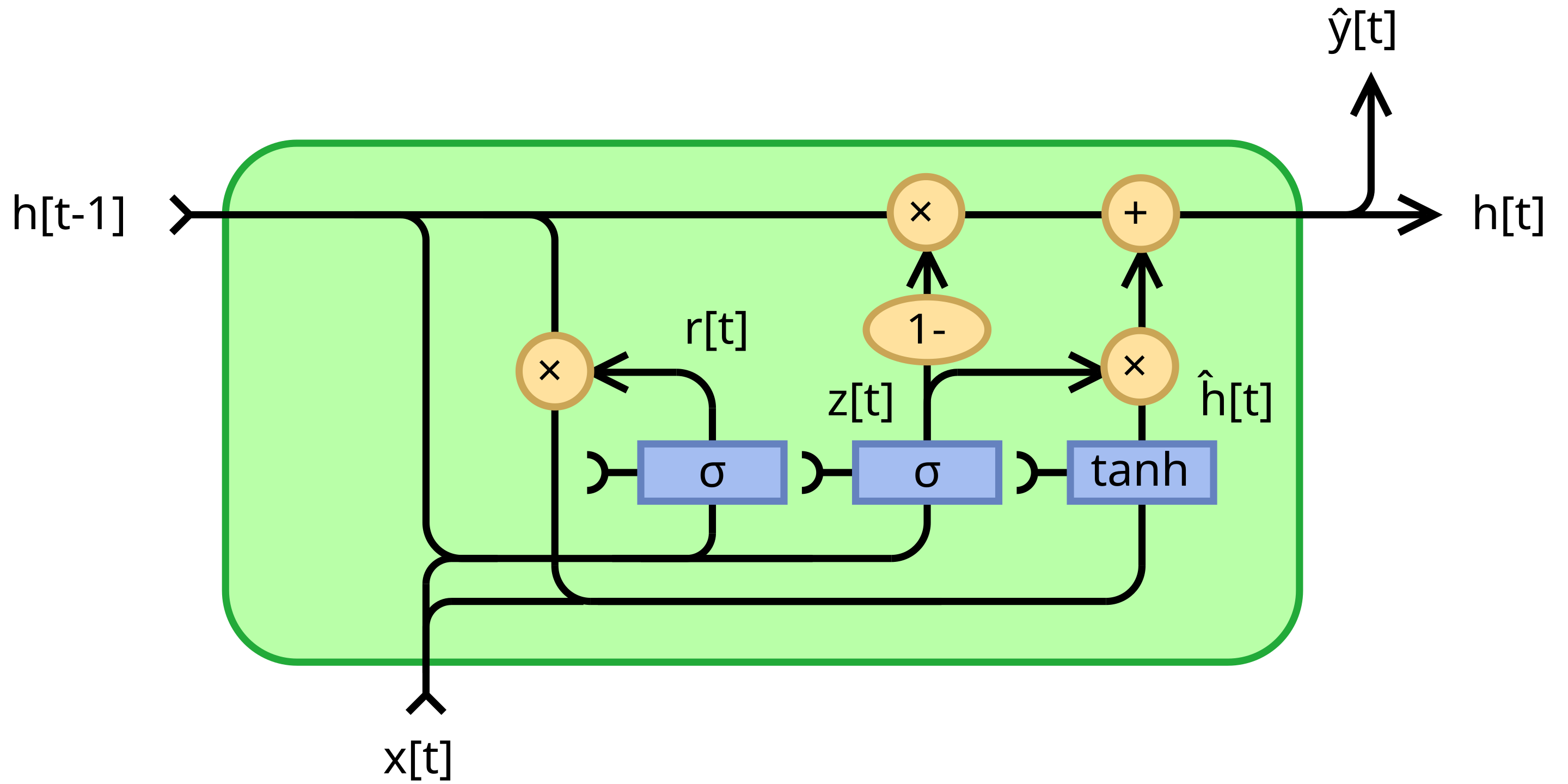
手写实现代码如下:
class GRURNN(nn.Module):
def __init__(self):
super().__init__()
# RNN 的权重矩阵
self.W_z = nn.Parameter(torch.randn(hidden_size, input_size)) # 输入权重
self.W_r = nn.Parameter(torch.randn(hidden_size, input_size)) # 输入权重
self.W_h = nn.Parameter(torch.randn(hidden_size, input_size)) # 输入权重
self.U_z = nn.Parameter(torch.randn(hidden_size, hidden_size)) # 隐藏状态权重
self.U_r = nn.Parameter(torch.randn(hidden_size, hidden_size)) # 隐藏状态权重
self.U_h = nn.Parameter(torch.randn(hidden_size, hidden_size)) # 隐藏状态权重
self.b_z = nn.Parameter(torch.zeros(hidden_size, 1)) # 偏置项
self.b_r = nn.Parameter(torch.zeros(hidden_size, 1)) # 偏置项
self.b_h = nn.Parameter(torch.zeros(hidden_size, 1)) # 偏置项
# 输出层
self.o_y = nn.Sequential(
nn.Linear(hidden_size, output_size),
nn.Sigmoid()
)
def forward(self, x, h_prev):
# https://en.wikipedia.org/wiki/Gated_recurrent_unit
# update gate vector
z = torch.sigmoid(self.W_z @ x + self.U_z @ h_prev + self.b_z)
# reset gate vector
r = torch.sigmoid(self.W_r @ x + self.U_r @ h_prev + self.b_r)
# candidate activation vector
h_tilde = torch.tanh(self.W_h @ x + self.U_h @ (r * h_prev) + self.b_h)
# next hidden state
h_next = (1 - z) * h_prev + z * h_tilde
# 输出层
y = self.o_y(h_next.T)
return y.T, h_next
关于天气的例子规则学习
通过相关 RNN GRU 或 RNN LSTM 的学习,可以让机器习得类似如下结果,完整代码参考:RNN GRU
采用 torch 官方的 GRU 实现,其模型定义就更为简单,如下:
# 官方 GRU 实现
class GRUModel(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super().__init__()
self.gru = nn.GRU(input_size, hidden_size, batch_first=True)
self.fc = nn.Sequential(nn.Linear(hidden_size, output_size), nn.Sigmoid())
def forward(self, x, hidden):
out, hidden = self.gru(x, hidden) # x: (batch, seq_len, input_size)
out = self.fc(out) # out: (batch, seq_len, hidden_size)
return out, hidden
模型预测结果:
sunny applepie ✅ [1.0, 0.0, 0.0] tensor([9.9932e-01, 1.7285e-03, 2.8279e-04])
rainy hamburger ✅ [0.0, 1.0, 0.0] tensor([3.5221e-04, 9.9963e-01, 4.1863e-04])
rainy chicken ✅ [0.0, 0.0, 1.0] tensor([4.5053e-04, 1.5327e-03, 9.9940e-01])
rainy applepie ✅ [1.0, 0.0, 0.0] tensor([9.9956e-01, 5.2562e-04, 5.6997e-04])
sunny applepie ✅ [1.0, 0.0, 0.0] tensor([9.9996e-01, 3.5776e-04, 5.8669e-05])
rainy hamburger ✅ [0.0, 1.0, 0.0] tensor([4.3072e-04, 9.9962e-01, 2.9802e-04])
sunny hamburger ✅ [0.0, 1.0, 0.0] tensor([3.1623e-04, 9.9990e-01, 1.7700e-04])
rainy chicken ✅ [0.0, 0.0, 1.0] tensor([3.6378e-04, 1.7131e-03, 9.9946e-01])
sunny chicken ✅ [0.0, 0.0, 1.0] tensor([2.0140e-04, 9.5274e-04, 9.9996e-01])
rainy applepie ✅ [1.0, 0.0, 0.0] tensor([9.9950e-01, 5.3829e-04, 6.4449e-04])
seq2seq
在掌握 RNN LSTM/GRU 之后,可以尝试一下 seq2seq,可以参考 Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention)
其核心思路是通过两个 RNN(一个 Encoder,一个 Decoder),来做句子的翻译:

图片来源:https://github.com/sooftware/seq2seq
- encoder 对原句子进行 RNN 计算,按每个词计算完成后,计算出最终的 encoder hidden status,相当于对原油的句子做了一整个句子的语义编码。对工程比较熟悉的同学,可以类比到 LLVM IR(或者是任何需要编译过程的中间代码,或者可以类比到语法树 AST)
- decoder 负责对 encoder hidden status 解码到另外一种语言(在工程领域可类比生成到二进制编码、或编程语言转译之类的 re-generator)
seq2seq 例子
为了方便生成测试数据,训练量少,可本地测试复现,所以找了一个加法的 seq2seq 例子,比如输入 “12+34” 这个字符串,输出 “46” 这个字符串。
测试数据
测试数据准备,对于加法算法,需要 0~9 这几个字符,然后是 + 字符。为了对其输入输出字符串的长度,需要有个填充字符,比如:_。最后,还需要有表示字符串开始和结束的字符,此处选择 { 和 }。所以,所有的字符如下(当然你也可以自由定义你自己的字符集合):
chars = "0123456789+_{}"
对应的测试数据集有:
输入:`12+34}` 输出:`_46}`
输入:`__2+3}` 输出:`__5}`
输入:`67+89}` 输出:`156}`
注意:开始字符
{仅在 decoder 的第一个字符才需要用到。
embedding
参考:What Are Word Embeddings for Text?
embedding 本质上是将「词汇」映射到「向量空间」的表征学习技术,使得词汇的含义能被向量表示。
比如下图所示,一个比较好的 embedding 模型,词汇能通过向量算法被预测出来,比如:
- Queen - Woman = King - Man
- Queen - King = Woman - Man
- 所以当计算 King - Man + Woman 时,模型能预测出是 Queen 这个单词

seq2seq 模型
Encoder,与之前烹饪算法类似,只是多了字符串的映射,因为此处模型的对象的字符串和词汇。
class Encoder(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
# 嵌入层:将字符索引转换为向量
self.embedding = nn.Embedding(input_size, hidden_size)
# RNN GRU:处理序列
self.gru = nn.GRU(hidden_size, hidden_size)
def forward(self, input_char, hidden):
# 改成 shape 为 [1, 1, hidden_size]
embedded = self.embedding(input_char).view(1, 1, -1)
# encoder 其实只需要使用 hidden_status,output 并不需要使用
_, hidden = self.gru(embedded, hidden)
return hidden
Decoder,与 Encoder 类似,多了 softmax,用于预测对所有已知字符的概率。
class Decoder(nn.Module):
def __init__(self, hidden_size, output_size):
super().__init__()
self.embedding = nn.Embedding(output_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size)
# 输出层:从隐藏状态预测下一个字符
self.out = nn.Linear(hidden_size, output_size)
# LogSoftmax 层:对输出进行对数softmax归一化,得到每个词的对数概率
self.logsoftmax = nn.LogSoftmax(dim=1)
def forward(self, input_char, hidden):
embedded = self.embedding(input_char).view(1, 1, -1)
output, hidden = self.gru(embedded, hidden)
# logsoftmax 至少是 2 维的
output = self.logsoftmax(self.out(output[0]))
return output, hidden
Seq2seq 模型,就是把上述 Encoder 和 Decoder 串联在一起,Encoder 最终输出的 hidden 就是 Decoder 初始化的 hidden,decoder 输入,初始化为开始字符(也就是 {),损失函数为分类任务的计算,与 logsoftmax 对应即可。
class Seq2Seq:
def __init__(self):
super().__init__()
# encoder & decoder
self.encoder = Encoder(chars_number, HIDDEN_SIZE)
self.decoder = Decoder(HIDDEN_SIZE, chars_number)
# 优化器,随机梯度下降
self.encoder_optimizer = optim.SGD(self.encoder.parameters(), lr=learning_rate)
self.decoder_optimizer = optim.SGD(self.decoder.parameters(), lr=learning_rate)
# 损失函数 NLLLoss 分类任务,与 decoder 的 LogSoftmax 对应
self.criterion = nn.NLLLoss()
def train(self, input_tensor, target_tensor):
# 把encoder的梯度清零,防止累积
self.encoder_optimizer.zero_grad()
self.decoder_optimizer.zero_grad()
# 隐藏状态
hidden = torch.zeros(1, 1, HIDDEN_SIZE)
# encoder
# 循环输入,输出 hidden_status
for input in input_tensor:
hidden = self.encoder(input, hidden)
# decoder
# Decoder 的第一个输入是 SOS 标记
decoder_input = torch.tensor(SOS_TOKEN_INDEX)
loss = 0
# 教师强制 (Teacher Forcing): 在训练时,使用真实的下一目标字符作为下一个输入
for target in target_tensor:
decoder_output, hidden = self.decoder(decoder_input, hidden)
# 计算损失
loss += self.criterion(decoder_output, target.unsqueeze(0))
# 将下一个输入设置为正确的答案(教师强制)
decoder_input = target
loss.backward()
self.encoder_optimizer.step()
self.decoder_optimizer.step()
return loss.item() / OUTPUT_LENGTH
预测
当训练完成后,相关的模型预测如下:
--- 模型评估 ---
输入: 12+35 | 真实值: 47 | 预测值: 47 | 结果: ✅ 正确
输入: 99+1 | 真实值: 100 | 预测值: 100 | 结果: ✅ 正确
输入: 50+50 | 真实值: 100 | 预测值: 100 | 结果: ✅ 正确
输入: 1+99 | 真实值: 100 | 预测值: 100 | 结果: ✅ 正确
输入: 60+89 | 真实值: 149 | 预测值: 149 | 结果: ✅ 正确
输入: 77+88 | 真实值: 165 | 预测值: 165 | 结果: ✅ 正确
输入: 10+20 | 真实值: 30 | 预测值: 30 | 结果: ✅ 正确
输入: 3+34 | 真实值: 37 | 预测值: 37 | 结果: ✅ 正确
输入: 12+35 | 真实值: 47 | 预测值: 47 | 结果: ✅ 正确
输入: 20+10 | 真实值: 30 | 预测值: 30 | 结果: ✅ 正确
输入: 40+50 | 真实值: 90 | 预测值: 90 | 结果: ✅ 正确
输入: 2+9 | 真实值: 11 | 预测值: 11 | 结果: ✅ 正确
正确率 100.00%
完整代码可参考 seq2seq gist
Attention
仔细观察上述的模型,可以发现非常大的一个问题,就是 decoder 只接受了 encoder 的最终语义,也就是这个最终语义要包含句子中的所有含义,那可想而知,如果句子非常长的话,这个 hidden 很可能就不够用了,为了解决这个问题,Attention 出现了。
注意力机制
同样是上述加法计算,在预测值的过程中,很显然 + 这个字符,并没那么重要,所以在输出字符的时候,需要关注不同的 encoder 状态(即关注不同的输入字符),比如再输出十位数字的时候,应该需要更关注输入中是否有十位,以及十位数具体是什么。
| 图1 | 图2 | 图3 |
|---|---|---|
 |
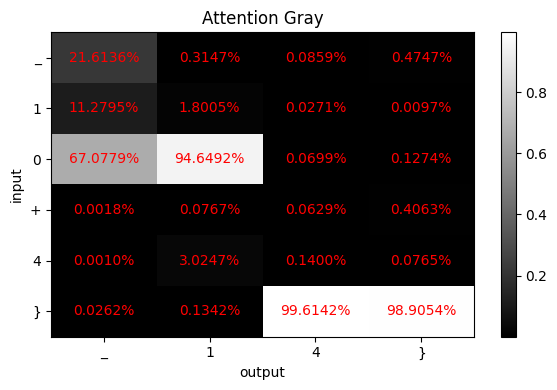 |
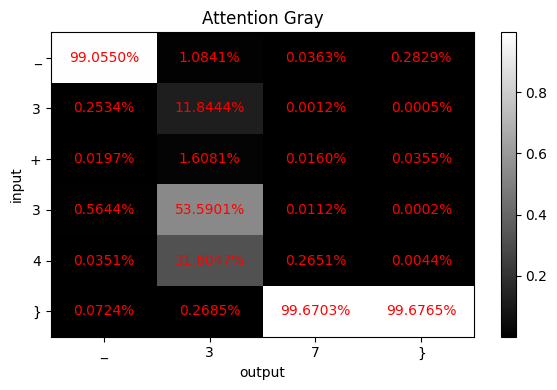 |
比如图 1 中的输入
10 + 20,输出为30的例子,字符串 3 的输出,需要关注 1 和 2,以及分别看后面的数字是否会有进位。
注意力机制有好几种,此处使用最为基础的 [Bahdanau_(additive)attention](https://en.wikipedia.org/wiki/Attention(machine_learning)#Bahdanau_(additive)_attention),数学定义如下:
- 第一步,先计算对齐分数(Alignment Score)
- 第二步,通过 softmax,计算注意力权重(Attention Weights)
- 第三步,使用权重对隐藏层加权求和,得到上下文向量(Context Vector)
注意力代码实现
class Attention(nn.Module):
def __init__(self, hidden_size):
super().__init__()
# 注意:Bahdanau 使用拼接 [s_{t-1}; h_i],所以输入维度是 enc_hidden_dim + dec_hidden_dim
self.W_a = nn.Linear(hidden_size * 2, hidden_size)
self.v_a = nn.Linear(hidden_size, 1, bias=False) # 输出标量 score
# encoder_hidden_states: [1, seq_len, hidden_size]
# decoder_hidden_state: [1, 1, hidden_size]
def forward(self, encoder_hidden_states, decoder_hidden_state):
# Step 0: prepare inputs,对齐输入
decoder_hidden_state_expanded = decoder_hidden_state.repeat(1, encoder_hidden_states.size(1), 1) # [1, seq_len, hidden_size]
inputs = torch.cat((encoder_hidden_states, decoder_hidden_state_expanded), 2) # [1, seq_len, 2*hidden_size]
# Step 1: socre each hidden state,计算对齐分数
energy = torch.tanh(self.W_a(inputs)) # (1, seq_len, hidden_size)
scores = self.v_a(energy).transpose(1, 2) # (1, 1, seq_len)
# Step 2: softmax the scores,计算注意力权重
softmax_scores = torch.softmax(scores, dim=2) # [1, 1, seq_len]
# Step 3. sum up by weights,计算 context 向量(加权和 encoder hidden states)
context_vector = torch.bmm(softmax_scores, encoder_hidden_states) # [1, 1, hidden_size]
return context_vector, softmax_scores
对 decoder 添加 attenion 注意力后,完整的代码如下:seq2seq with attention
小结
从 RNN 出发,通过 GRU 学习一个最简单的烹饪规则学习算法,熟悉整体的 RNN 逻辑,最重要的就是序列化输入的隐藏状态理解。两个 GRU RNN(Encoder + Decoder)就组成了一个最基本的 seq2seq,主要用于语言翻译,此处通过一个加法字符串的例子,成功地让机器学习了加法规则。最后为了解决长字符串的问题,引入的 Attention 机制,从而实现了更好的模型拟合能力。
References
- The Illustrated Transformer
- Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention)
- 循环神经网络(RNN)
- PyTorch 循环神经网络(RNN)
- A friendly introduction to Recurrent Neural Networks
- Long short-term memory
- Gated recurrent unit
- Seq2seq
- What Are Word Embeddings for Text?
- Attention_(machine_learning)