一元线性回归已经包含了巨多的基础知识，且能串联出很多之前的内容，所以有必要做个笔记。翻看我之前的笔记，关于AI的一些想法已经是 8 年前的事了，没想到 Deep Learnin 之 Hello World Demo、XOR 简单实现也已经都是 4、5 年前的事了。

命题和定义

已知部分房屋面积和房屋价格的一个数据集，如何建立模型，对一个新的房屋面积，预测房屋价格？

模型假设

假设房屋面积和房屋价格是线性相关的，则可以建立如下模型： $y = \theta_0 + \theta_1 x$

此处的模型假设，非常有意思，为什么的自变量是 $x$，而不是 $x^2$, $sin(x)$ 呢？这其实很考验你对模型的假设关系。

这里有个 tensorflow playground 的例子非常有意思。下图是对两个数据集的简单分类器，只有一层神经网络。所以，假设模型其实分别是：

\[output_{1} = bias + weight_{1} x_{1} + weight_{2} x_{2}\]

\[output_{2} = bias + weight_{1} x_{1} ^2 + weight_{2} x_{2} ^2\]

可以看到仅是单层神经网络，其模型假设和一元线性回归没有什么大的差异，本质上差不多，都考验着你对模型的假设关系。从上述两个例子来看，$x^2$ 并没有给模型假设带来什么增量帮助（即更贴合真实模型，更快的收敛速度，降低模型迭代成本）。

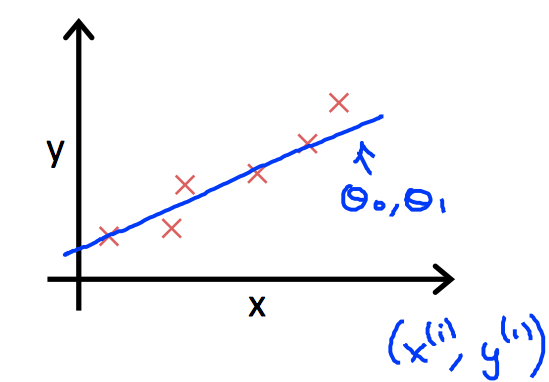
所以，从模型假设的经验来看，$y = bias + weight_{1} x_{1}$ 也就是一开始的模型假设：$y = \theta_0 + \theta_1 x$，已经够用，也够拟合目标数据集了。因为我们的数据集是这样的：

PS：其一元模型假设，其实已经对应神经网络的单个神经元了，其中 $bias$ 就是 $\theta_0$, $weight$ 就是 $\theta_1$

如果数据集模型的假设是类似 $x^2$ 或 $sin(x)$ 的，则模型假设需要依据事实做相关调整。

不过，这样的模型假设就真的很考验能力了，因为实际的情况远比这个复杂，比如有 100 多个自变量的情况，那么模型假设就需要考虑更多，这就远非是 $x_1$ 还是 $x_1^2$ 这么简单了。

还好，后续我们有了深度学习，多层神经网络，从实践表明，足够多的 hidden layer 就可以拟合较为复杂的数据集，比如：

PS：对 hidden 应该需要多少层合适，每层的神经元数应该多少合适，也考验着对模型假设的能力，一般来说，在计算资源够用的情况下，越多的层，越多的神经元，其拟合模型的能力越强。

损失函数是用来评估模型是否拟合数据集，其损失函数的计算公式为：

\[J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^i) - y^i)^2\]

其中损失函数的定义，也比较有意思，其中最关键的是 $(h_\theta(x^i) - y^i)^2$

PS: $x^i$ 为什么用上标，是因为要和后续的矩阵做区分，$x^i_j$ 表示矩阵的第 $i$ 行第 $j$ 列的值

假设数据集的第一个数据为 $(x_1, y_1)$，假设函数为 $y = \theta_0 + \theta_1 x$

转成公式 $\theta_1x - y + \theta_0 = 0$，由点到线的距离可知：

\[PQ = \frac{|\theta_1 x - y + \theta_0|} {\sqrt{(\theta_1)^2 + (-1)^2}}\]

标准的损失函数应该如上述 PQ 距离的表达，但是，这里我们使用的是 $(h_\theta(x^i) - y^i)^2$，只是一个近似参考值，为了表达方便。

其中 $\frac{1}{2m}$ 中的 $m$ (与 $\sum_{i=1}^m$ 相消) 和 $\frac{1}{2}$（与平方相消）是为了求偏导的时候的方便。