前端神经网络初学者，捣鼓 XOR 逻辑运算，之前很多东西都浮于“看”，很多细节没有“实践”，所以借此机会再回顾和使用一下原来所学。

背景

来自 @夕山 大佬的灵感，看到 《神经网络的演进史》 以及对逻辑运算的训练过程，神经网络的程序入门（Js 版） ，核心代码如下：

var log = console.log;

var Perceptron = function() { // 感知器
  this.step=function(x, w) { // 步阶函数：计算目前权重 w 的情况下，网路的输出值为 0 或 1
    var result = w[0]*x[0]+w[1]*x[1]+w[2]*x[2]; // y=w0*x0+x1*w1+x2*w2=-theta+x1*w1+x2*w2
    if (result >= 0) // 如果结果大于零
      return 1;      //   就输出 1
    else             // 否则
      return 0;      //   就输出 0
  }
  
  this.training=function(truthTable) { // 训练函数 training(truthTable), 其中 truthTable 是目标真值表
    var rate = 0.01; // 学习调整速率，也就是 alpha
    var w = [ 1, 0, 0 ]; 
    for (var loop=0; loop<1000; loop++) { // 最多训练一千轮
      var eSum = 0.0;
      for (var i=0; i<truthTable.length; i++) { // 每轮对于真值表中的每个输入输出配对，都训练一次。
        var x = [ -1, truthTable[i][0], truthTable[i][1] ]; // 输入： x
        var yd = truthTable[i][2];       // 期望的输出 yd
        var y = this.step(x, w);  // 目前的输出 y
        var e = yd - y;                  // 差距 e = 期望的输出 yd - 目前的输出 y
        eSum += e*e;                     // 计算差距总和
        var dw = [ 0, 0, 0 ];            // 权重调整的幅度 dw
        dw[0] = rate * x[0] * e; w[0] += dw[0]; // w[0] 的调整幅度为 dw[0]
        dw[1] = rate * x[1] * e; w[1] += dw[1]; // w[1] 的调整幅度为 dw[1]
        dw[2] = rate * x[2] * e; w[2] += dw[2]; // w[2] 的调整幅度为 dw[2]
        if (loop % 100 == 0)
          log("%d:x=(%s,%s,%s) w=(%s,%s,%s) y=%s yd=%s e=%s", loop, 
               x[0].toFixed(3), x[1].toFixed(3), x[2].toFixed(3), 
               w[0].toFixed(3), w[1].toFixed(3), w[2].toFixed(3), 
               y.toFixed(3), yd.toFixed(3), e.toFixed(3));
      }
      if (Math.abs(eSum) < 0.0001) return w; // 当训练结果误差够小时，就完成训练了。
    }
    return null; // 否则，就传会 null 代表训练失败。
  }
}

function learn(tableName, truthTable) { // 学习主程式：输入为目标真值表 truthTable 与其名称 tableName。
  log("================== 学习 %s 函数 ====================", tableName);
  var p = new Perceptron();       // 建立感知器物件
  var w = p.training(truthTable); // 训练感知器
  if (w != null)                  // 显示训练结果
    log("学习成功 !");
  else
    log("学习失败 !");
  log("w=%j", w);
}

var andTable = [ [ 0, 0, 0 ], [ 0, 1, 0 ], [ 1, 0, 0 ], [ 1, 1, 1 ] ]; // AND 函数的真值表
var orTable  = [ [ 0, 0, 0 ], [ 0, 1, 1 ], [ 1, 0, 1 ], [ 1, 1, 1 ] ]; // OR  函数的真值表
var xorTable = [ [ 0, 0, 0 ], [ 0, 1, 1 ], [ 1, 0, 1 ], [ 1, 1, 0 ] ]; // XOR 函数的真值表

learn("and", andTable); // 学习 AND 函数
learn("or",  orTable);  // 学习 OR  函数
learn("xor", xorTable); // 学习 XOR 函数

理论上，背后求出的 weight 其实就是对上述真值表的线性划分（盗图自 @夕山 大佬 😂）：

但是以上的单层感知器，能成功学习 AND 和 OR 函数，但是 XOR 就很无能为力，原因也很简单，从几何学的角度，XOR 的分布无法从单条线性函数进行聚合分类。

搞事情

因为之前也捣鼓过 DeepLearning 的 手写识别 相关的 Demo，所以想决定加个隐藏层来实现 xor 操作，从理论上讲，加一层隐藏 Layer 之后，将原有 XOR 矩阵做一次转换映射之后，便能做进一步的线性划分了。类似以下：

我们通过加一层 2 维空间隐藏层，将 XOR 映射为上图中的第二个真值表，于是我们就能愉快地分割了 😂

XOR 第一版 JS

第一版的代码在 Github Gist, 具体的就不放在文中，核心思路是对原有 @夕山 大佬的代码叠加一层隐藏层。反向传播用的也是 朴素的按照误差修正，对我来说依旧是迷一样的存在：

dw[0] = rate * x[0] * e; w[0] += dw[0];

相关文档在 脉络清晰的BP神经网络讲解。

虽然学习成功有一定的概率，但也是歪打正着。不过，这依旧是一次非常不错的实践，以至于能从中启发我画出上面的那张图，最简单的原理性图，也就是二次的矩阵映射。

简单贴一下运行结果吧

后面括号中的，就是二次映射的结果，比如：

xor: [0, 0] => [1,0], [0, 1] => [1, 1], [1, 0] => [0, 0], [1, 1] => [1, 0]

======== 第 5 次学习 ========
 学习 and 函数成功：
loop= 341730  w1:  [[0.39963790000397476,33.63402299979549,-0.9887426000058843],[-0.20303059999641215,0.41553599999999374,-0.41543859999487487]]  w2:  [0.0009000000000003372,-0.0010000000000000763,-0.0005999999999999929]
0 and 0 =  0 ( [ 0, 0, 1 ] , [ 0, 0, 1 ] )
0 and 1 =  0 ( [ 0, 1, 1 ] , [ 1, 1, 1 ] )
1 and 0 =  0 ( [ 1, 0, 1 ] , [ 0, 0, 1 ] )
1 and 1 =  1 ( [ 1, 1, 1 ] , [ 1, 0, 1 ] )
 学习 or 函数成功：
loop= 244  w1:  [[0.5519268,-0.06474380000000002,-0.06840439999999995],[-0.49513199999999985,-1.0470319999999997,0.558002]]  w2:  [0.39760000000000023,-0.5260999999999998,0.13020000000000032]
0 or 0 =  0 ( [ 0, 0, 1 ] , [ 0, 1, 1 ] )
0 or 1 =  1 ( [ 0, 1, 1 ] , [ 0, 0, 1 ] )
1 or 0 =  1 ( [ 1, 0, 1 ] , [ 1, 1, 1 ] )
1 or 1 =  1 ( [ 1, 1, 1 ] , [ 1, 0, 1 ] )
 学习 xor 函数成功：
loop= 696460  w1:  [[-0.7513457000000062,0.35677259999999433,0.39457490000601025],[-36.21090990031919,35.48711019926247,-0.06928969999966195]]  w2:  [-0.000299999999999751,0.001400000000000198,0.00010000000000053716]
0 xor 0 =  0 ( [ 0, 0, 1 ] , [ 1, 0, 1 ] )
0 xor 1 =  1 ( [ 0, 1, 1 ] , [ 1, 1, 1 ] )
1 xor 0 =  1 ( [ 1, 0, 1 ] , [ 0, 0, 1 ] )
1 xor 1 =  0 ( [ 1, 1, 1 ] , [ 1, 0, 1 ] )

XOR 第二版 JS

因为第一版存在一定的学习成功概率，激活函数是 0-1 函数，也没有用比较常规的反向传播。所以，心里总有些咯噔，想用之前学的，简单做个实践，不用任何库和框架，就最简单的网络结构。实现一下理论中的

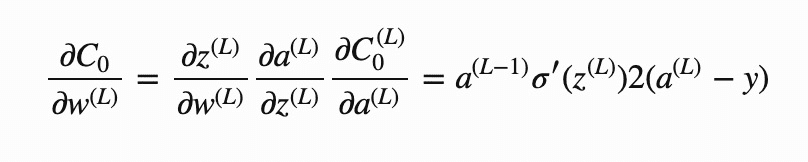
于是有了如下代码：


var random = () => {
  return +(Math.random() * 2 - 1).toFixed(4);
};

// 激活函数
function sigmoid(x) {
  return 1 / (1 + Math.pow(Math.E, -x));
}

// sigmoid 导数
function sigmoidDerivative(x) {
  return sigmoid(x) * (1 - sigmoid(x));
}

class Perceptron {

  constructor(name = 'xor', showResult = true, showCost = false) {

    this.name = name;
    this.showResult = showResult;
    this.showCost = showCost;

    if (name === 'and') {
      this.inputs = [[ 0, 0], [0, 1], [1, 0], [1, 1]]; // 输入值
      this.outputs = [[1, 0], [1, 0], [1, 0], [0, 1]]; // 期望结果
    } else if (name === 'or') {
      this.inputs = [[ 0, 0], [0, 1], [1, 0], [1, 1]]; // 输入值
      this.outputs = [[1, 0], [0, 1], [0, 1], [0, 1]]; // 期望结果
    } else {
      this.inputs = [[ 0, 0], [0, 1], [1, 0], [1, 1]]; // 输入值
      this.outputs = [[1, 0], [0, 1], [0, 1], [1, 0]]; // 期望结果
    }

    this.rate = 10;

    // 随机初始化所有权重
    this.w1 = [[ random(), random(), random()], [random(), random(), random()]];
    this.w2 = [[ random(), random(), random()], [random(), random(), random()]];

    this.loopTimes = 1000;
  }

  // 向前计算
  forward(x, w) {
    // 1 * w[2] = b
    return sigmoid(x[0] * w[0] + x[1] * w[1] + 1 * w[2]);
  }

  // sigmoid 求导
  derivative(x) {
    // 入参为 sigmoid 之后的数值，直接传入即可
    return x * (1 - x);
  }

  // 损失函数
  cost(y, e) {
    let sum = 0;
    for (let i = 0; i < y.length; i++) {
      sum += (y[i] - e[i]) * (y[i] - e[i]);
    }
    return sum / y.length;
  }

  // 验证
  verify() {
    const { inputs, outputs, w1, w2 } = this;

    console.log(`\n学习 ${this.name} 的逻辑结果：`)
    for (let i = 0; i < inputs.length; i++) {
      var expect = outputs[i];
      var input = inputs[i];
      var h = [
        this.forward(input, w1[0]),
        this.forward(input, w1[1]),
      ];
      var y = [
        this.forward(h, w2[0]),
        this.forward(h, w2[1]),
      ];

      console.log(`${input[0]} ${this.name} ${input[1]} = ${y[0] > 0.5 ? 0 : 1}  (0 的概率：${(y[0] * 100).toFixed(2)}, 1 的概率：${(y[1] * 100).toFixed(2)})`);
    }
  }

  // 训练
  training() {
    const { inputs, outputs, w1, w2, rate, derivative, loopTimes } = this;

    for (var loop = 0; loop < loopTimes; loop++) {

      var deltaW2 = [[0, 0, 0], [0, 0, 0]];
      var deltaW1 = [[0, 0, 0], [0, 0, 0]];
      var costSum = 0;

      for (let i = 0; i < inputs.length; i++) {
        var expect = outputs[i];
        var input = inputs[i];

        // 隐藏层（中间结果）
        var h = [
          this.forward(input, w1[0]),
          this.forward(input, w1[1]),
        ];

        // 计算结果（预测结果）
        var y = [
          this.forward(h, w2[0]),
          this.forward(h, w2[1]),
        ];

        // 计算损失值
        const c = this.cost(y, expect);
        costSum += c;

        // 反向传播第一层
        deltaW2[0][0] += (y[0] - expect[0]) * derivative(y[0]) * h[0];
        deltaW2[0][1] += (y[0] - expect[0]) * derivative(y[0]) * h[1];
        deltaW2[0][2] += (y[0] - expect[0]) * derivative(y[0]);

        deltaW2[1][0] += (y[1] - expect[1]) * derivative(y[1]) * h[0];
        deltaW2[1][1] += (y[1] - expect[1]) * derivative(y[1]) * h[1];
        deltaW2[1][2] += (y[1] - expect[1]) * derivative(y[1]);

        // 反向传播第二层
        const deltaSumH1 = (
          (y[0] - expect[0]) * derivative(y[0]) * w2[0][0] +
          (y[1] - expect[1]) * derivative(y[1]) * w2[1][0]
        );
        const deltaSumH2 = (
          (y[0] - expect[0]) * derivative(y[0]) * w2[0][1] +
          (y[1] - expect[1]) * derivative(y[1]) * w2[1][1]
        );

        deltaW1[0][0] += deltaSumH1 * derivative(h[0]) * input[0];
        deltaW1[0][1] += deltaSumH1 * derivative(h[0]) * input[1];
        deltaW1[0][2] += deltaSumH1 * derivative(h[0]);

        deltaW1[1][0] += deltaSumH2 * derivative(h[1]) * input[0];
        deltaW1[1][1] += deltaSumH2 * derivative(h[1]) * input[1];
        deltaW1[1][2] += deltaSumH2 * derivative(h[1]);
      }

      if (this.showCost) {
        console.log(costSum)
      }

      // 平均之后修正
      for (let i = 0; i < 2; i++) {
        for (let j = 0; j < 3; j++) {
          w1[i][j] -= rate * (deltaW1[i][j] / inputs.length);
        }
      }

      for (let i = 0; i < 2; i++) {
        for (let j = 0; j < 3; j++) {
          w2[i][j] -= rate * (deltaW2[i][j] / inputs.length);
        }
      }
    }

    if (this.showResult) {
      this.verify();
    }
  }
}


var andP = new Perceptron('and');
andP.training();

var orP = new Perceptron('or');
orP.training();

var xorP = new Perceptron('xor');
xorP.training();

// var xorP = new Perceptron('xor', false, true);
// xorP.training();

结果输出：


学习 and 的逻辑结果：
0 and 0 = 0  (0 的概率：99.85, 1 的概率：0.14)
0 and 1 = 0  (0 的概率：98.60, 1 的概率：1.43)
1 and 0 = 0  (0 的概率：98.68, 1 的概率：1.27)
1 and 1 = 1  (0 的概率：2.50, 1 的概率：97.51)

学习 or 的逻辑结果：
0 or 0 = 0  (0 的概率：98.30, 1 的概率：1.67)
0 or 1 = 1  (0 的概率：1.49, 1 的概率：98.53)
1 or 0 = 1  (0 的概率：1.49, 1 的概率：98.53)
1 or 1 = 1  (0 的概率：0.79, 1 的概率：99.25)

学习 xor 的逻辑结果：
0 xor 0 = 0  (0 的概率：96.34, 1 的概率：3.62)
0 xor 1 = 1  (0 的概率：3.15, 1 的概率：96.87)
1 xor 0 = 1  (0 的概率：3.15, 1 的概率：96.87)
1 xor 1 = 0  (0 的概率：96.22, 1 的概率：3.74)

多次实验后，发现稳定性和效果比第一版要好很多，在实践中，最令人绝望的，无非就是反向传播那块，好在有非常棒的学习资源，主要有：

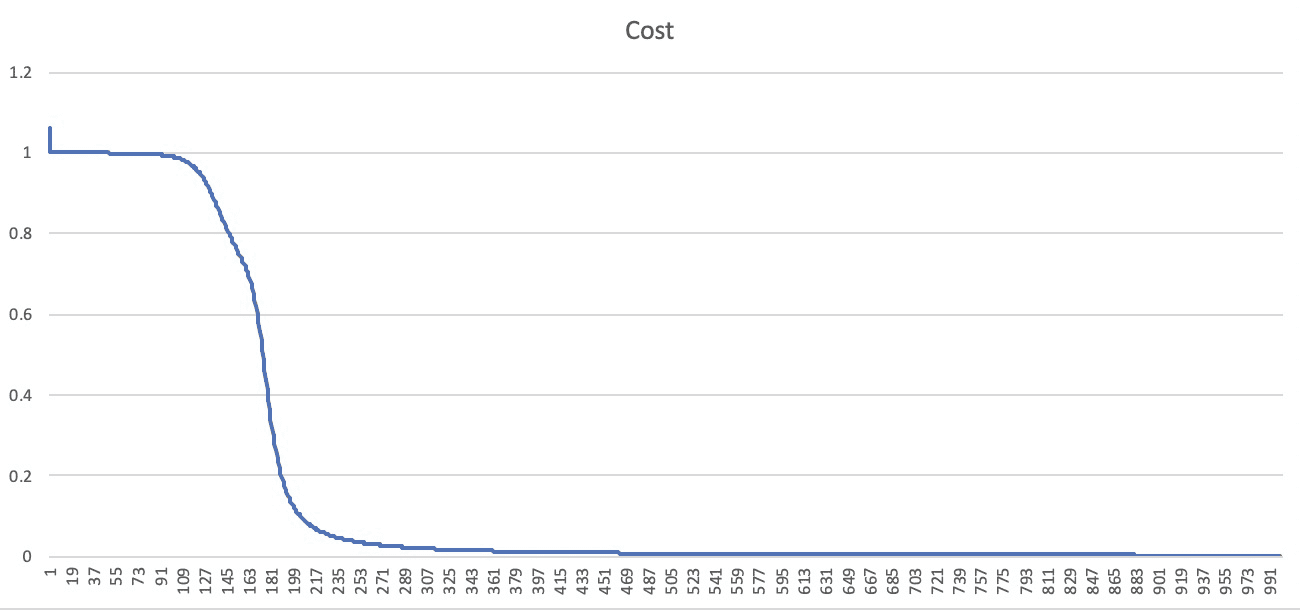
梯度下降效果

我们通过计算 cost 值，可以看到以下曲线，在训练近 200 次的时候，已经开始趋于平缓了，非常优雅的一条曲线，大爱~

后记

最原理性和最基础的有较深的了解后，算是会写 Hello World 了吧。😂

参考