• 梯度下降
  • 反向传播

梯度下降 (gradient descent)

假设两个分量 $v1$，$v2$，计算 Cost Function

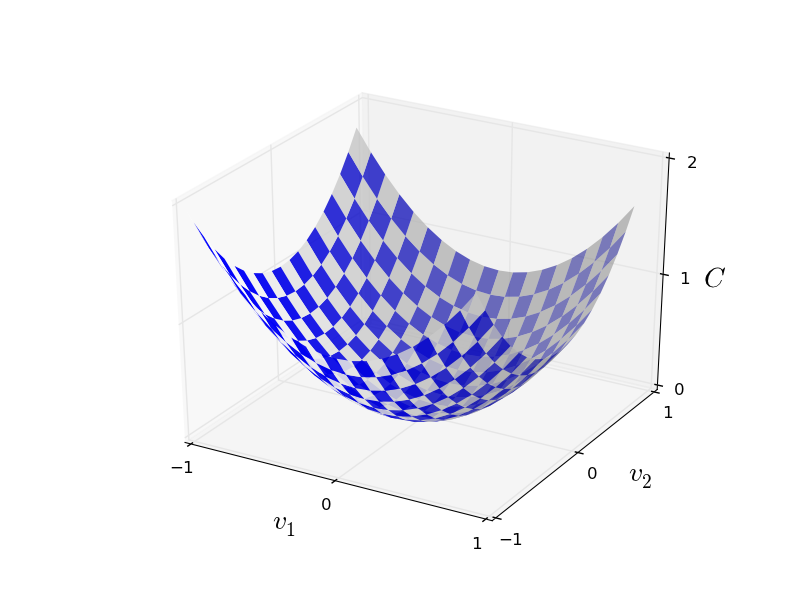
如上图所示，每次 $\Delta C$ (Delta C) 的变化有：

\[\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2. \tag{7}\end{eqnarray}\]

标记 $\nabla C$ (Nabla C) 梯度向量（gradient vector）为

\[\begin{eqnarray} \nabla C \equiv \left( \frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2} \right)^T \equiv \begin{pmatrix} \frac{\partial C}{\partial v_1} \\ \frac{\partial C}{\partial v_2} \end{pmatrix} \tag{8}\end{eqnarray}\]

标记 $\Delta v \equiv (\Delta v_1, \Delta v_2)^T$， 则公式 7 可改写为

\[\begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v \tag{9}\end{eqnarray}\]

可将 $\Delta v $ 改写为以下方式，其中 $\eta$ 为学习率 ( learning rate )

\[\begin{eqnarray} \Delta v = -\eta \nabla C, \tag{10}\end{eqnarray}\]

由上可得 $\Delta C \approx -\eta \nabla C \cdot \nabla C = -\eta |\nabla C|^2$ ，也可以看到位置 $v$ 到 $v’$ 的变化公式

\[\begin{eqnarray} v \rightarrow v' = v -\eta \nabla C. \tag{11}\end{eqnarray}\]

反向传播微积分部分

建设一个每层仅有一个的神经网络，如下所示

axx

我们可以按上图得到

\[Cost \rightarrow C(...) = (a^{(L)} - y)^2 \\ denote \rightarrow z^{(L)} = w^{(L)}a^{(L - 1)} + b^{(L)}\\ a^{(L)} = \sigma z^{(L)}\]

以上三个公式的关系如下图所示

20190714104053

我们希望计算出 $w^{(L)}$ 最终对 $C_0$ 的变化影响，也就是求对 $C_0$ 的 $w^{(L)}$ 的偏导数

\[\frac{\partial C_0}{\partial w^{(L)}} = \frac{\partial z^{(L)}}{\partial w^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial C_0^{(L)}}{\partial a^{(L)}}\]

以上各个偏导数计算如下：

\[C_0 = (a^{(L)} - y)^2 \Rightarrow \frac{\partial C_0^{(L)}}{\partial a^{(L)}} = 2(a^{(L)} - y) \\ a^{(L)} = \sigma z^{(L)} \Rightarrow \frac{\partial a^{(L)}}{\partial z^{(L)}} = \sigma'(z^{(L)}) \\ z^{(L)} = w^{(L)}a^{(L - 1)} + b^{(L)} \Rightarrow \frac{\partial z^{(L)}}{\partial w^{(L)}} = a^{(L - 1)} \\\]

所以

\[\frac{\partial C_0}{\partial w^{(L)}} = \frac{\partial z^{(L)}}{\partial w^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial C_0^{(L)}}{\partial a^{(L)}} = a^{(L - 1)} \sigma'(z^{(L)}) 2(a^{(L)} - y)\]

References