PID 算法简记
PID 算法是在工程领域,运用最为广泛的调节器,记录一下位式控制算法和 PID 算法的区别,以及 PID 各个参数对 SV 的影响。
PID 控制器
A proportional–integral–derivative controller (PID controller or three term controller) is a control loop feedback mechanism widely used in industrial control systems and a variety of other applications requiring continuously modulated control. A PID controller continuously calculates an error value {\displaystyle e(t)}
as the difference between a desired setpoint (SP) and a measured process variable (PV) and applies a correction based on proportional, integral, and derivative terms (denoted P, I, and D respectively), hence the name.
PID 控制器是一种在工业领域广泛使用的循环控制系统,PID 控制器需要持续计算 SetPoint 和 ProcessVariable 之间差值,记为 e(t),然后通过比例 P,积分 I,微分 D 三个部分来优化输出达到目标值。
位式控制算法
位式控制算法
- 通过用户设置(按键或可调电阻)一个期望值 sv
- 通过位式控制算法,输出out 高低点平
- 通过out 输出,利用执行部件控制控制对象
- 控制对象做相关动作
- 传感器获得相关传感参数后,输出当前值 pv,然后位式控制算法通过 sv 和 pv 对比,输出 out 值

我们以温度控制为例,用户设置 100 摄氏度的 sv 预期值,当 pv 低于 100 摄氏度的时候,位式控制算法输出高电位,执行部件打开开关,控制对象(加热器)开始加热,直到传感器感知到温度大于 100 摄氏度的时候,out 为低电平,停止加热即可。
特点
位式控制算法的特点是:
- out 只有 H、L 两种电位
- out 输出依据
- pv < sv ==> H
- pv >= sv ==> L
局限
由于控制对象的惯性,比如加热器的通电之后,并不会马上达到加热效果,关闭电源后,加热器还有余温会去加热,也不会马上达到降温的效果,所以,由于控制对象的惯性,pv 会在 sv 水位上下浮动,我们期望这个浮动更可能小。
PID 算法

比例控制算法 - P
历史采样值:X1, X2, … Xk-1, Xk
当前偏差:Ek = Sv - Xk (Sv 为用户期望值)
- 大于 0 表示当前未达标
- 等于 0 表示当前已达标
- 小于 0 表示当前已超标
输出:Pout = Kp * Ek + Out0 (Out0 是为了控制在 Ek 为 0 的时候,使得 Out 不为 0 的常数 ,Kp 为比例系数)
特点:
out 输出并不只是高低电平两种可能,而是 PWM 信号,该信号有一个信号控制周期,可以在一个周期内,控制多少时间导通,多少时间关闭。具体的控制精度由 PWM 的脉宽决定。
缺点:只考虑现在,不考虑偏差
积分算法 - I
历史偏差序列:E1, E2, … Ek-1, Ek
Sk = E1 + E2 + … Ek-1 + Ek (因为 Ek 有可能是正数,也可能是负数,该代数和并不会是一个正无穷)
- 大于 0,过去这段时间大部分是未达标
- 等于 0
- 小于 0,过去这段时间大部分是超标
Iout = Ki * Sk + Out0
特点:考虑了历史数据,没有充分考虑现在的偏差
微分算法 - D
最近偏差:Dk = Ek - E k-1
- 大于 0,偏差正越来越大,偏差有增大的趋势,变化率
- 等于 0,偏差没有发生改变
Dout = Kd * Dk + Out0, 微分是用来预测将来的变化,由于等于 0 的时候,代表着偏差没有发生变化,只要 Dk 为 0, Dout 就会为 0,这样不会输出信号,所以微分不能单独用于输出信号。
PID 各个参数的影响
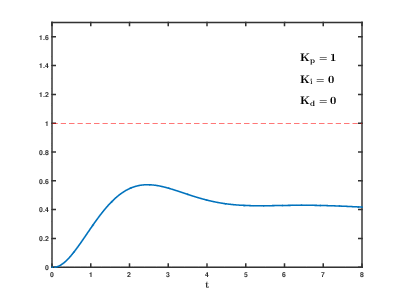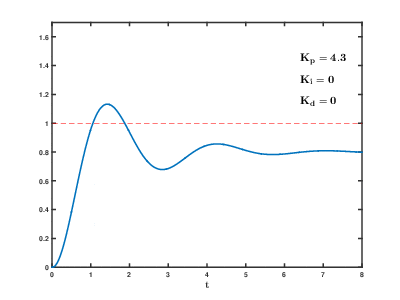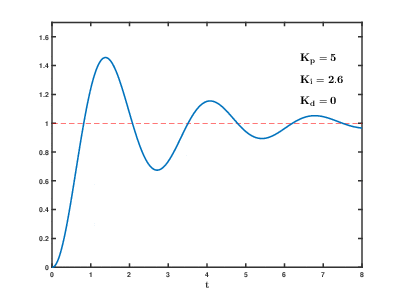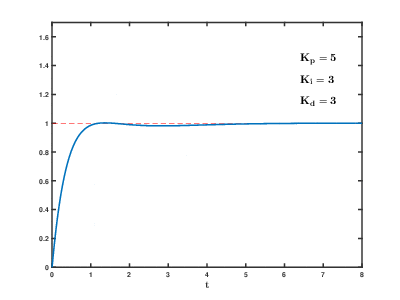
Comments
Leave a comment